Ortsvektor Bedeutung Viereck

Question

Aufgabe: ich habe ein gleichschenkliges Dreieck gegeben mit den Punkten A,B und C und muss nun den Punkt D ermitteln, so dass das Dreieck zum Quadrat wird. Warum ist der Ortsvektor zu D der gleiche Ortsvektor wie zu A?

Answer 1

Warum ist der Ortsvektor zu D der gleiche Ortsvektor wie zu A?

Ich denke dann hast du etwas falsch verstanden. Wenn A = D gilt, dann hast du ja immer noch kein Viereck.

Mach doch mal ein Foto von der Exakten Aufgabe oder Schreibe sie ab.

Comments

A(5,5,0), B(0,2,4), C(-5,5,0), bestimmen Sie die Koordinaten eines weiteren Punktes D, so dass das Viereck ein Quadrat ist

---

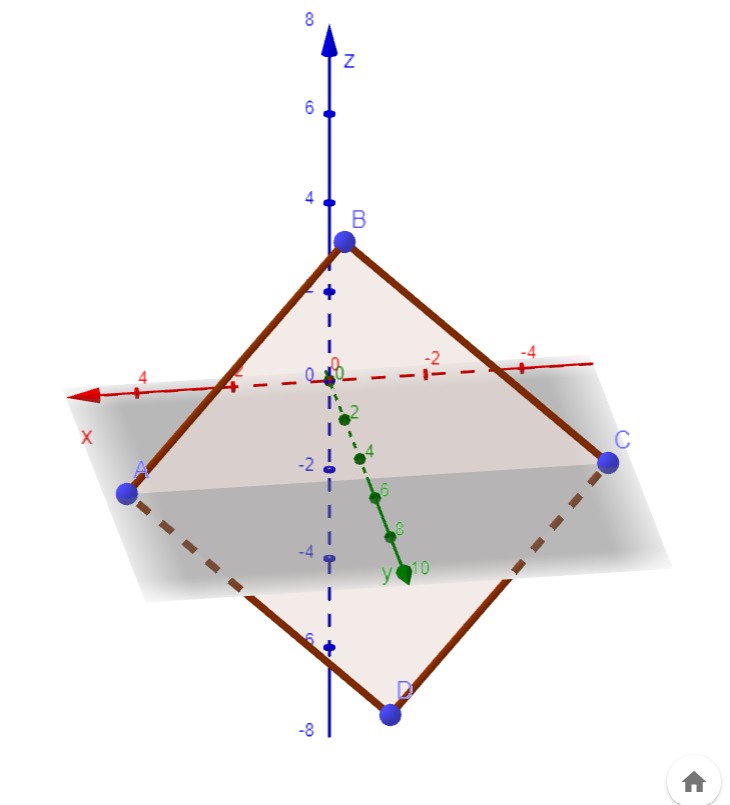
|AB| = |[0, 2, 4] - [5, 5, 0]| = |[-5, -3, 4]| = √(5^2 + 3^2 + 4^2)
|BC| = |[-5, 5, 0] - [0, 2, 4]| = |[-5, 3, -4]| = √(5^2 + 3^2 + 4^2)

AB·BC = [-5, -3, 4]·[-5, 3, -4] = 0

AD = BC
D - A = BC
D = A + BC = [5, 5, 0] + [-5, 3, -4] = [0, 8, -4]

Der Punkt D lautet damit: D(0 | 8 | -4).

Skizze

---

Super danke, die haben nur in den Lösungen den Ortsvektor von A und den Ortsvektor von D gleichgesetzt und mir fehlt das Verständnis warum die beiden Ortsvektoren gleich sind. Könnten die Ortsvektoren zu B & C auch die gleichen sein oder ist das abhängig von der Skizze, die ich mir dann machen würde?

---

Also ist der Ortsvektor zu den Eckpunkten immer der gleiche oder ist es von der Skizze beziehungsweise von den Koordinaten abhängig?

---

Die haben vermutlich nicht die Ortsvektoren gleichgesetzt. Auch die Ortsvektoren von B und C sind nicht gleich. Das sieht man ja schon, weil sie gegeben sind.

Evtl. haben sie Beträge von Richtungsvektoren gleichgesetzt.

Aber ich denke, mein angewandtes Verfahren wäre hier das einfachste. Zunächst zeige ich, dass AB und BC gleich lang sind und einen rechten Winkel einschließen. Dann kann man das Dreieck ABC mit dem Punkt D zu einem Quadrat ABCD erweitern.

---

Also ist der Ortsvektor zu den Eckpunkten immer der gleiche oder ist es von der Skizze beziehungsweise von den Koordinaten abhängig?

Ich verstehe dich nicht. Hier sind keine Punkte und keine Ortsvektoren gleich.

Es gilt das im Dreieck ABCD gegenüberliegende Seiten parallel und gleich lang sind und damit gilt für die Richtungsvektoren AD = BC. Das sind aber Richtungsvektoren und keine Ortsvektoren.

---

Ihre Variante wäre doch auch sicherer oder?

---

Ja. Ich finde das beinahe Idiotensicher :)