Wie hoch ist die Brücke?

Question

Aufgabe: Der abgebildete Brückenbogen lässt sich mit folgender Funktionsgleichung beschreiben:

f(x) = 69 - 0,007·x²

Der Koordinatenursprung wurde in Höhe der Wasseroberfläche senkrecht unter Scheitel der Parabel gelegt.

a) Wie hoch ist die Brücke?

b) Der Abstand des eingezeichneten Punktes Q zur y-Achse ist 30 m. Wie hoch liegt der Punkt Q über der Wasseroberfläche?

c) Wie breit ist die Brücke an der Wasseroberfläche

Comments

Abbildung fehlt.

---

abgebildete Brückebogen ... des eingezeichneten Punktes Q

Da ist nix abgebildet und nix eingezeichnet.

unter Scheitel der Parabel

Y= 0,007x*2 +69 ist keine Parabel. Zur Verdeutlichung:

Geschrieben hast Du die erste Funktion (blau eingezeichnet). Hast Du die zweite gemeint?

---

kontolliere bitte die Funktionsgleichung, fehlt da nicht ein Minus?

Answer 1

a)

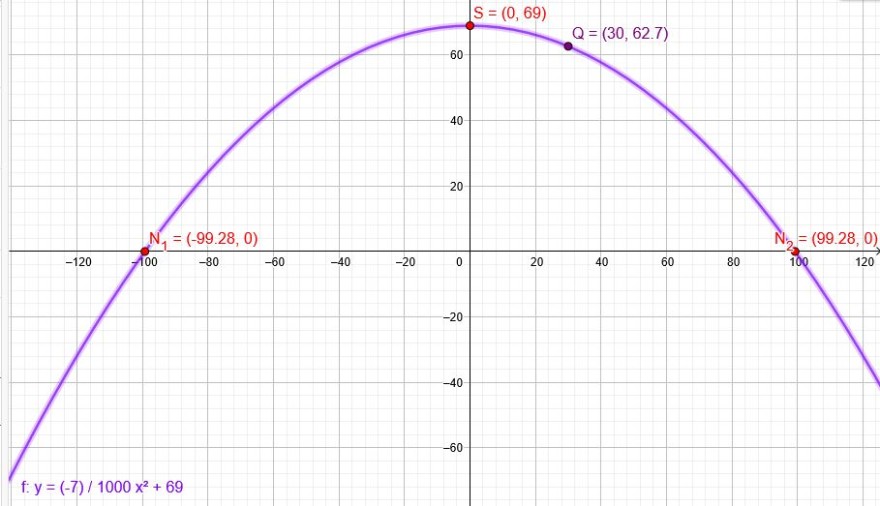
$y= -0,007x^2 +69$      $y(0)= -0,007\cdot 0^2 +69$  Die Brücke ist 69m hoch.

b)

$y=- 0,007 \cdot 30^2 +69=62,7$  Der Punkt Q liegt 62,7m über der Wasseroberfläche.

c)

$0= -0,007x^2 +69$         $x_1≈-99,2831$       $x_2≈99,2831$  

Die Brücke ist ungefähr $|-99,2831|+99,2831=198,5662$m breit.