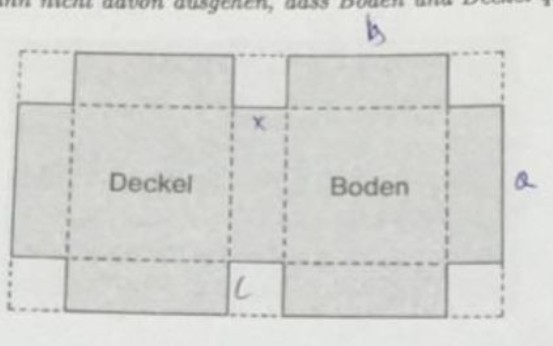
Von einem rechteckigen, \( 40 \mathrm{~cm} \) langen und \( 20 \mathrm{~cm} \) breiten \( S t u c k \) Pappe werden wie in der Abbildung erkennbar Quadrate abgeschnitten. Berechnen Sie, wie groß sind diese zu wählen, damit der Rest der eine Schachtel mit möglichst großem Inhalt ergibt, deren Deckel auf drei Seiten tabergreift?
Hinweis: Man kann nicht davon ausgehen, dass Boden und Deckel quadratisch sind.