Aufgabe:
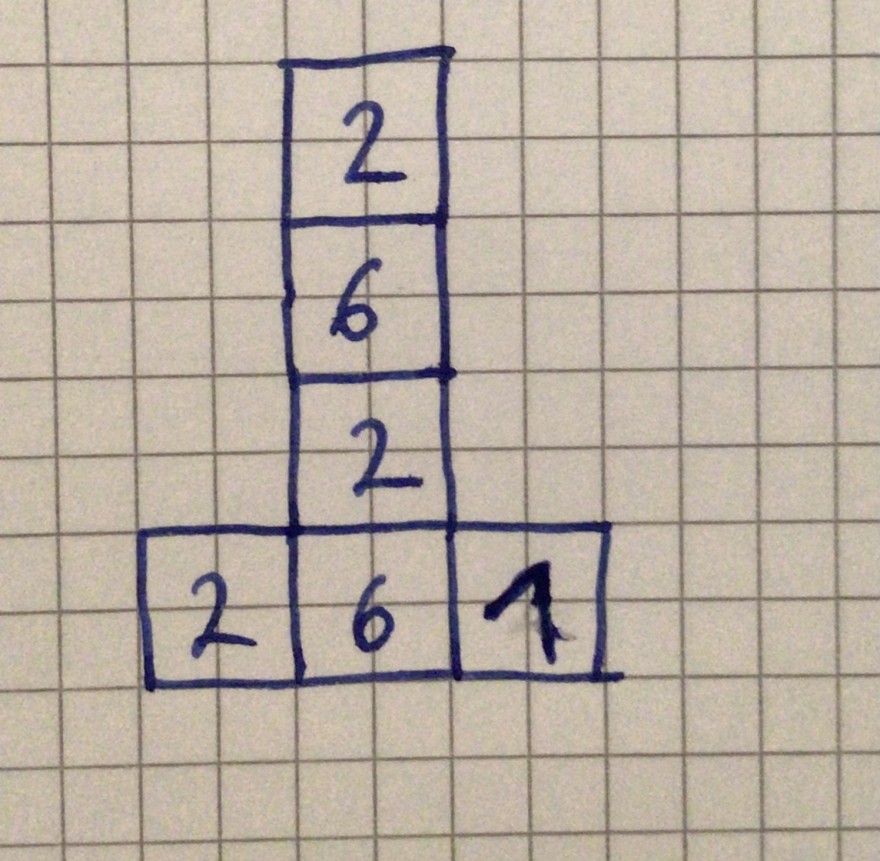
Im Folgenden wird mit einem Würfel ge-worfen, der das rechts abgebildete Netz mit den Ziffern 1, 2 und 6 besitzt.
a) Der Würfel wird zweimal geworfen.
Berechnen Sie die Wahrscheinlichkeiten für die folgenden Ereignisse:
* A: „Genau eine Sechs wird gewürfelt"
* B: „Zwei verschiedene Ziffern fallen"
b) Wie oft muss der Würfel mindestens ge-worten werden, damit mit einer Wahrscheinlichkeit von wenigstens 85% mindestens eine Sechs fällt?
c) Der Würfel wird sechsmal geworfen. Wie wahrscheinlich ist es, dass eine Ziffernfolge fällt, die genau 2 Sechsen, 2 Zweien und 2 Einsen enthält?
d)Der Würfel wird 12-mal geworfen? Wie viele Einsen, Zweien und Sechsen sind zu er-warten? Wie groß ist die Wahrscheinlichkeit, dass
E1: genau 6 Zweien, E2: mindestens 2 Einer, E3: höchstens 10 Zweien,
E4: nur Zweien und Sechsen gewürfelt werden?
Problem/Ansatz:
Für a) habe ich P(A)= 44% und P(B)=61% raus. Bei b) habe ich n=5.
Bei c) und d) Weiß ich leider überhaupt nicht weiter. Ich wäre wirklich sehr dankbar für sämtliche Unterstützung, da diese Ausarbeitung von mir sehr zeitnah bewertet wird.
Vielen Dank im Voraus!
(Ich habe das Würfelnetz zum Verständnis einmal aufgemalt)