Sternschnuppen und Poissonverteilung

Question

Aufgabe:

(a) An einem Winterabend werden durchschnittlich sechs Sternschnuppen pro Stunde beobachtet. Dabei kann davon ausgegangen werden, dass die Anzahl \( X_{t} \) der in \( t \) Minuten beobachteten Sternschnuppen poissonverteilt ist mit dem Parameter \( \lambda= \) \( t / \alpha(\alpha>0) \).

(i) Bestimmen Sie \( \alpha \).

Problem/Ansatz:

Aufgabe 2, bin ich so richtig vorgegangen? Habe die 60 wegen 60 min eingesetzt und die 6 dann entsprechend für t

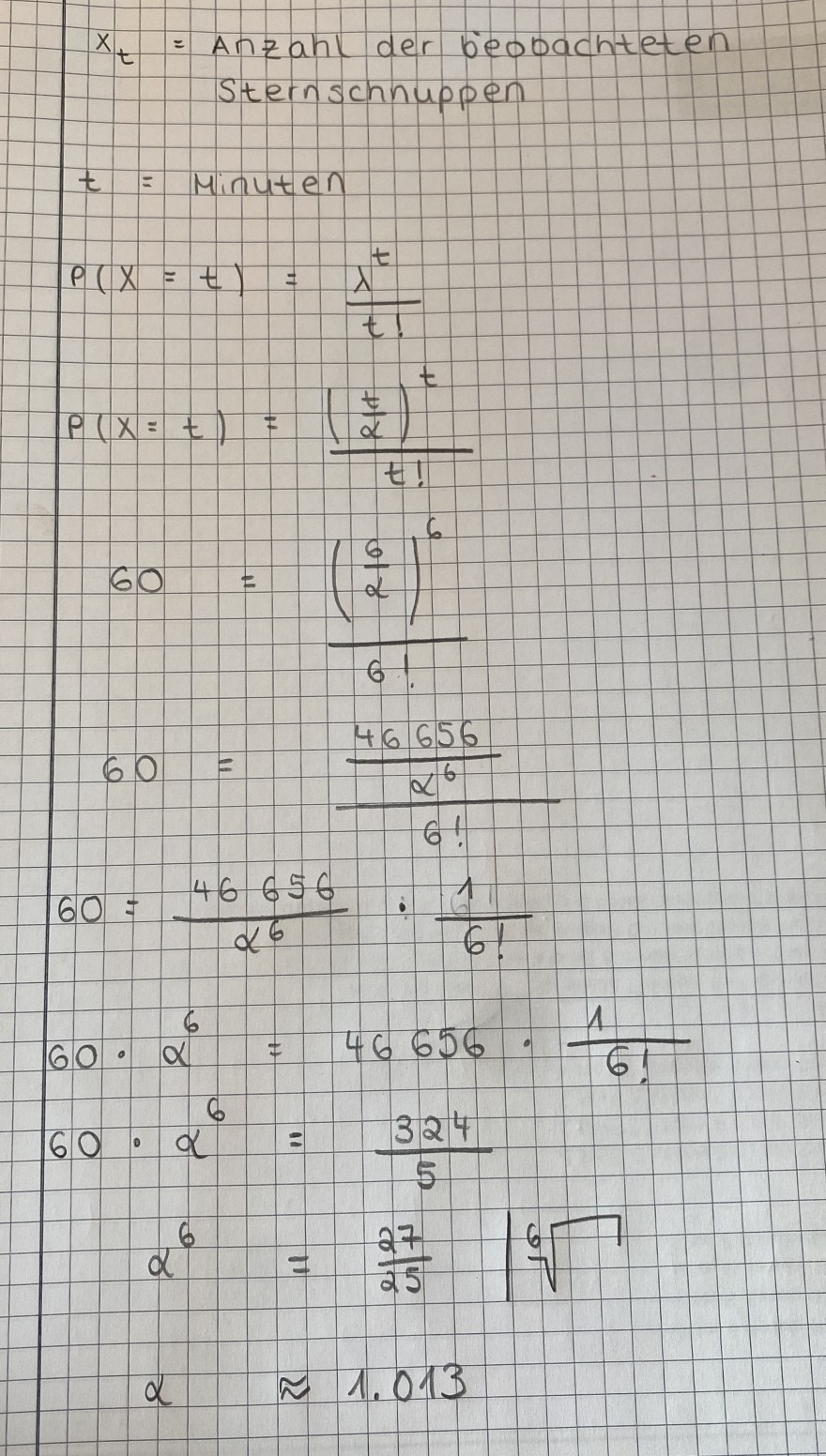
Text erkannt:

\( \begin{array}{l}x_{t}=\text { Anzahl der beooachteten } \\ \text { Sternschnuppen } \\ t=\text { Minuten } \\ P(X=t)=\frac{\lambda^{t}}{t!} \\ p(x=t)=\frac{\left(\frac{t}{\alpha}\right)^{t}}{t!} \\ 60=\frac{\left(\frac{6}{2}\right)^{6}}{6!} \\ 60=\frac{\frac{46656}{\alpha^{6}}}{6!} \\ 60=\frac{46656}{\alpha^{6}} \cdot \frac{1}{6!} \\ 60 \cdot \alpha^{6}=46656 \cdot \frac{1}{6!} \\ 60 \cdot \alpha^{6}=\frac{324}{5} \\ \left.\alpha^{6}=\frac{27}{25} \right\rvert\, \sqrt[6]{7} \\ \alpha \approx 1.013 \\\end{array} \)

Answer 1

Das passt nicht, denn \(P(X=t)\) ist eine Wahrscheinlichkeit und kann damit nicht 60 betragen. Arbeite hier mit dem Erwartungswert. In 60 Minuten erwarten wir 6 Sternschuppen, also gilt \(E[X_{60}]=\lambda_{60}=6=\frac{60}{\alpha}\) nach Aufgabenstellung.

Answer 2

λ = t / α --> α = t / λ = 60 / 6 = 10

Der Parameter α sollte also den Wert 10 haben.