Die Schnittgerade zweier Ebenen bestimmen

Question

Aufgabe: Schnittgerade zweier Ebenen bestimmen

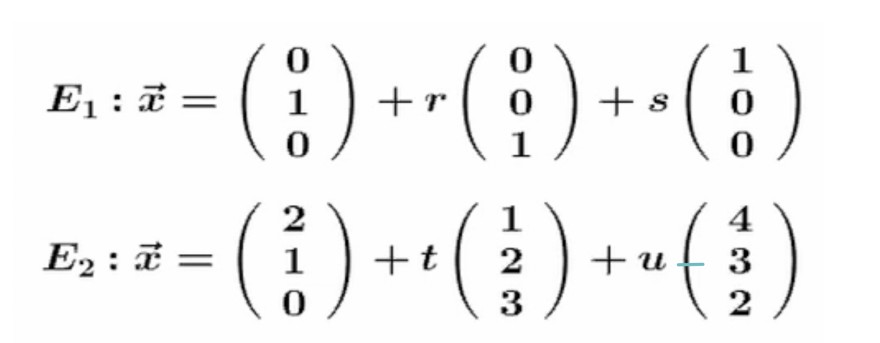
Text erkannt:

$\begin{array}{l}E_{1}: \vec{x}=\left(\begin{array}{l}0 \\ 1 \\ 0\end{array}\right)+r\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right)+s\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right) \\ E_{2}: \vec{x}=\left(\begin{array}{l}2 \\ 1 \\ 0\end{array}\right)+t\left(\begin{array}{l}1 \\ 2 \\ 3\end{array}\right)+u\left(\begin{array}{l}4 \\ 3 \\ 2\end{array}\right)\end{array}$

Ansatz:

Text erkannt:

Ebenen greionsetzen $\rightarrow$ umgefoumt:
$r \cdot\left(\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right)+s \cdot\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right)+t \cdot\left(\begin{array}{l} -1 \\ -2 \\ -3 \end{array}\right)+u \cdot\left(\begin{array}{l} -4 \\ -3 \\ -2 \end{array}\right)=\left(\begin{array}{l} 2 \\ 0 \\ 0 \end{array}\right)$

Gaup-Verfahren:
$\begin{array}{l} \left(\begin{array}{cccc|c} r & s & t & u & \\ 0 & 1 & -1 & -4 & 2 \\ 0 & 0 & -2 & -3 & 0 \\ 1 & 0 & -3 & -2 & 0 \end{array}\right) \Leftrightarrow\left(\begin{array}{cccc|c} p & s & t & 4 & \\ 1 & 0 & -3 & -2 & 0 \\ 0 & 1 & -1 & -4 & 2 \\ 0 & 0 & -2 & -3 & 0 \end{array}\right) \\ \text { II. }-2 t-3 u=01+3 u \\ \begin{array}{c} -\alpha t=3 u 1:(-\alpha) \\ t=-1,5 u \end{array} \xrightarrow{\text { in } E_{2}} E: \vec{x}=\left(\begin{array}{l} 2 \\ 1 \\ 0 \end{array}\right)-1,5 u \cdot\left(\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right)+u \cdot\left(\begin{array}{l} 4 \\ 3 \\ 2 \end{array}\right) \\ \Leftrightarrow\left(\begin{array}{c} 2 \\ 1 \\ 0 \end{array}\right)+\left(\begin{array}{c} -1.54 \\ -34 \\ -4.54 \end{array}\right)+\left(\begin{array}{l} 44 \\ 34 \\ 2 u \end{array}\right) \\ \Leftrightarrow\left(\begin{array}{l} 2 \\ 1 \\ 0 \end{array}\right)+\left(\begin{array}{c} 2,54 \\ 0 \\ -2,54 \end{array}\right) \Leftrightarrow \underline{\left(\begin{array}{l} 2 \\ 1 \\ 0 \end{array}\right)+u\left(\begin{array}{c} 2,5 \\ 0 \\ -2,5 \end{array}\right)} \end{array}$

Ist die Schnittgerade richtig bestimmt worden?

Comments

Es gibt auch Seiten zur Kontrolle für Gleichungssysteme z.B. diese:

https://www.arndt-bruenner.de/mathe/scripts/gleichungssysteme.htm

Answer 1

Aloha :)

Alle Punkte der Ebene $E_1$ haben den $y$-Wert $1$.

Du brauchst also von der Ebene $E_2$ nur alle Punkte auszuwählen, für die $y=1$ gilt:$$1\stackrel!=1+2t+3u\implies u=-\frac23t$$Das setzt du in die Ebenengleichung $E_2$ ein und erhältst die Schnittgerade:$$g\colon\vec x=\begin{pmatrix}2\\1\\0\end{pmatrix}+t\begin{pmatrix}1\\2\\3\end{pmatrix}-\frac23t\begin{pmatrix}4\\3\\2\end{pmatrix}=\begin{pmatrix}2\\1\\0\end{pmatrix}+\frac{5t}{3}\begin{pmatrix}-1\\0\\1\end{pmatrix}$$

Da $t\in\mathbb R$ beliebig gewählt werden darf, könntest du noch $\frac{5t}{3}$ durch eine beliebige reelle Variable ersetzen, aber das ist Kosmetik.

Du hast eine mögliche Darstellung der Schnittgeraden richtig berechnet.$\quad\checkmark$

Comments

Die Darstellung einer Geradengleichung in Parameterform ist nicht eindeutig:

$$\vec x=\begin{pmatrix}2\\1\\0\end{pmatrix}+t\begin{pmatrix}\frac52\\[1ex]0\\[1ex]-\frac52\end{pmatrix}=\begin{pmatrix}2\\1\\0\end{pmatrix}+\pink{\frac{5t}{2a}}\begin{pmatrix}a\\0\\-a\end{pmatrix}\quad;\quad t\in\mathbb R$$

Für $a$ kannst du jede reelle Zahl $\ne0$ einsetzen. Der pinke Vorfaktor kann jeden beliebigen reellen Wert annehmen, da die Variable $t$ jeden beliebigen rellen Wert annehmen kann. Daher kannst du den pinken Vorfaktor durch eine reelle Variable ersetzen, z.B. durch $\lambda$. Wählst du noch $a=-1$ erkennst du, dass deine Darstellung der Schnittgeraden gleichwertig zu meiner Darstellung ist:$$\vec x=\begin{pmatrix}2\\1\\0\end{pmatrix}+\lambda\begin{pmatrix}-1\\0\\1\end{pmatrix}\quad;\quad \lambda\in\mathbb R$$

Answer 2

Vorgehen ist in Ordnung. Aber wieso gegen Ende $\iff$? Mach dir den Unterschied zu $=$ klar.

Du kannst dein Ergebnis selbst prüfen, wähle zwei einfache Punkte auf der Geraden und prüfe, ob diese Punkte in beiden Ebenen liegen. Das geht schneller als du vielleicht denkst. Wenn das für beide Punkte erfüllt ist, liegt auch die Gerade in beiden Ebenen.

Answer 3

Hallo.

Dein Ergebnis ist richtig. Ich habe nur dein Rechenweg nicht ganz verstanden. Hier ist nochmal eine etwas kompaktere Version von mir:

Ich bezeichne mal hier die Variablen bischen anders.