Berechne die Schnittpunkte der linearen Funktionen ft (x) = -2/t x + 4 -1/t

Question

ich wäre sehr dankbar wenn ihr mir helfen könntet, da unsere Lehrerin uns diese Aufgabe aufgeben hat um daraus eine Note zu machen. Dazu hat sie erwähnt, dass wir dies noch nicht hatten und so jeden Fragen sollten der uns helfen könnte das auszurechnen.

 

Kt ist das Schaubild der linearen Funktion

ft(x)=− 2/t x + 4 − 1/t       ;  x€R ;        t€R*

a) Untersuche Kt auf Schnittpunkte mit den Koordinatenachsen.
b) Bestimme t so, dass Kt eine Ursprungsgerade ist.
c) Für welchen Wert von t liegt der Punkt B(4;− 4/3) auf Kt.
d) Bestimme den gemeinsamen Punkt aller Schargeraden mit der t1 und t2 Methode.

 

Danke schonmal:)

Juli

Comments

 t€R*  heisst bestimmt  t€R⁺

Wenn ja, resultieren nur negative Geradensteigungen.

---

Ich glaube R* bezeichnet hier in Anlehnung an N* die Menge R \ {0}. Zumindest hatte ich es so gedeutet.

Answer 1

ft(x)= -2/t * x + 4 - 1/t

a) Untersuche Kt auf Schnittpunkte mit den Koordinatenachsen.

Y-Achsenabschnitt f(0)

f(0) = 4 - 1/t

Nullstellen f(x) = 0

-2/t * x + 4 - 1/t = 0
x - 2t + 1/2 = 0
x = 2t - 1/2

b) Bestimme t so, dass Kt eine Ursprungserade ist.

f(0) = 0

4 - 1/t = 0
4t - 1 = 0
4t = 1
t = 1/4

c) Für welchen Wert von t liegt der Punkt B(4;− 4/3) auf Kt.

f(4) = -4/3

-2/t * 4 + 4 - 1/t = -4/3
-8/t + 4 - 1/t = -4/3
-8 + 4t - 1 = -4/3 t
16/3 t = 9
t = 27/16

d) Bestimme den gemeinsamen Punkt aller Schargeraden mit der t1 und t2 Methode.

-2/t * x + 4 - 1/t = -2/s * x + 4 - 1/s
-2s * x + 4st - s = -2t * x + 4st - t
2tx -2sx = s - t
x(2t - 2s) = s - t
x = (s - t) / (2t - 2s) = -1/2

-2/t * (-1/2) + 4 - 1/t = 1/t - 1/t + 4 = 4

Der Gemeinsame Punkt lautet P(-1/2 | 4)

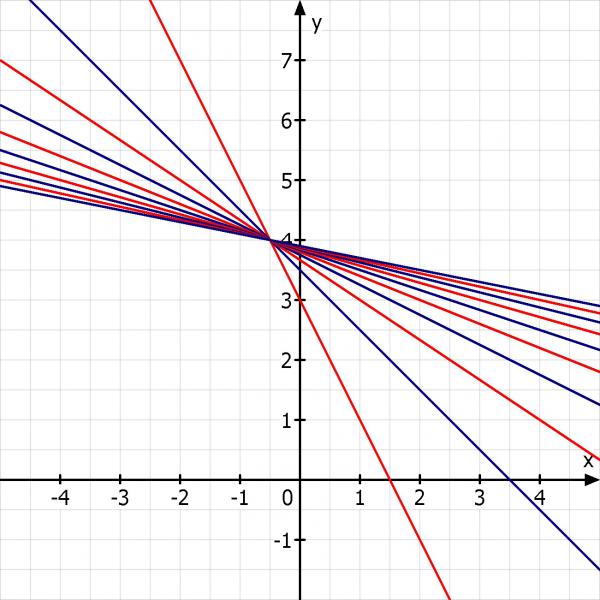
Skizze