Aufgabe:
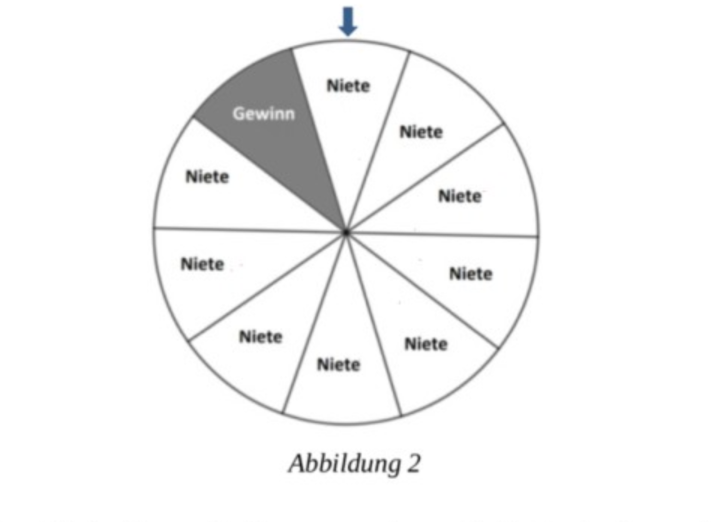
Bei einem Stadtfest gibt es ein Glücksrad, welches in zehn gleich große Sektoren unterteilt ist (siehe Abbildung 2). Jede teilnehmende Person dreht das Glücksrad genau einmal.
(1) Beschreiben Sie in diesem Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit mit dem folgenden Term berechnet werden kann:
\(\displaystyle \binom{7}{0} \cdot 0,1^{0} \cdot 0,9^{7}+\binom{7}{1} \cdot 0,1^{1} \cdot 0,9^{6}+\binom{7}{2} \cdot 0,1^{2} \cdot 0,9^{5} \)
(2) Geben Sie einen Term an, mit dem die Wahrscheinlichkeit für das folgende Ereignis berechnet werden kann: „Von 20 teilnehmenden Personen erhalten genau vier Personen einen Gewinn. "
(3) Ein anderes Glücksrad ist in \( n \) gleich große Sektoren aufgeteilt. Zwei Personen drehen dieses Glücksrad jeweils genau einmal. Die Zufallsgröße \( X \) gibt die Anzahl der Personen an, die einen Gewinn erhalten. Es gilt: \( P(X=0)=9 \cdot P(X=2) \). Ermitteln Sie eine mögliche Gesamtzahl n der Sektoren auf dem Glücksrad sowie die zugehörige Anzahl der Sektoren mit einem Gewinn.
Problem/Ansatz:
(1) "Von 7 teinehmenden Personen erhalten weniger gleich zwei Personen einen Gewinn"
(2) \(\displaystyle P(x=4)=\binom{20}{4} \cdot 0,1^{4} \cdot 0,9^{3} \)
Sind die Aufgaben 1-2 richtig ? Und wie gehe ich bei Aufgabe 3 vor?