Flugbahn mit Form einer halben Parabel + Brücken + Weitsprung (Parabeln und Quadratische Funktionen)

Question

Nachdem ich (auch dank eurer Hilfe) nun endlich die Grundlagen der quadratischen Funktionen verstanden habe, habe ich heute neue Aufgaben gefunden, bei denen ich aber überhaupt nicht weiß, wie ich z.B. Geschwindigkeit und etc. mit einbeziehen soll. Ich wäre euch unheimlich dankbar.

Aufgabe 1:

Gemeinsame Punkte von Funktionsgraphen: Anwendungen der quadratischen Funktionen und Gleichungen

Wirft man einen Gegenstand parallel zur Erde, so hat seine Flugbahn die Form einer halben Parabel. Die Gleichung dieser Parabel hat die Form \( y = −ax^2 + h \).

Fur den Wert von a gilt: \( a \approx \frac{5}{v^2} \)

Dabei ist v die Abwurfgeschwindigkeit (in m/s), x die Entfernung vom Abwurfpunkt in vertikaler Richtung (in m) und y die Höhe (in m), h ist die Abwurfhöhe (in m).

(a) Ein Flugzeug, das mit der Geschwindigkeit von 180 km/h (relativ zur Erde) fliegt, wirft ein Versorgungspaket ab. Wie weit von dem linken Baum entfernt landet das Paket?

Quelle: https://btmdx1.mat.uni-bayreuth.de/smart/gym/j09/funktion9/quad_anwend/gempunkt/gempunkt.pdf

b) Bei dem Springbrunnen tritt das Wasser aus dem Rohr mit der Geschwindigkeit 3,5 m/s aus. Wie weit muss der Rand des Wasserbeckens mindestens von der Rohröffnung entfernt sein?

Aufgabe 2:

Brücken: Viele moderne Brücken haben die Form von Parabeln. Die Abbildung zeigt die Müngstener Brücke bei Solingen aus den fünfziger Jahren. Legt man ein Koordinatensystem in den Scheitel des Bogens, so hat die Parabel die Gleichung \( y=-\frac{1}{9} x^{2} \) Die Bogenhöhe betriagt \( 69 \mathrm{m} \). Berechne die Spannweite.

Aufgabe 3:

Weitsprung: Bob Beamon sprang bei seinem Weltrekord bei den Olympischen Spielen 1968 in Mexiko-City \( 8,90 \mathrm{m} \) weit. Sein Körperschwerpunkt legte dabei in etwa die Bahn einer Parabel zurück, die angenähert durch die Gleichung \( y=-0,0571 x^{2}+0,3838 x+ 1,14 \) beschrieben wird. \( y \) gibt die jeweilige Höhe des Körperschwerpunktes über der Sprungrube (in \( m \)) und \( x \) die horizontale Entfernung von der Ausgangslage beim Absprung (in \( m \)) an. Hätte Bob Beamon bei seinem Weltrekord einen VW-Golf übersprungen?

Answer 1

1a)

Gesucht ist die Nullstelle der Wurfparabel, denn dort, wo das Versorgungspaket aufschlägt, hat es die Höhe 0, also muss die Parabelfunktion dort den Wert y = 0 liefern.

Da in Metern gerechnet wird, muss zunächst noch die Geschwindigkeit 180 km/h in die Einheit m/s umgerechnet werden: 180 km/h = 180000 m / 3600 s = 50 m/s

Mit

y = 0
h = 500 und
a = 5 / v ² = 5 / ( 50 ² ) = 5 / 2500

ergibt sich dann aus der allgemeinen Form y = - a x ² + h der Wurfparabel:

0 = - ( 5 / 2500 ) x ² + 500

Auflösen nach x:

<=> ( 5 / 2500 ) x ² = 500

<=> x ² = 250000

<=> x = ± √ 250000

<=> x = ± 500

Da vorliegend nach rechts , also in positive x-Richtung geschaut werden soll, ist die Lösung:

x = 500

Also: Das Versorgungspaket landet 500 m rechts vom linken Baum.

 

1b)

Kann nicht berechnet werden, da Angaben zur Geometrie des Springbrunnens fehlen, insbesondere zur Höhe der Austrittsöffnung der Wasserdüse. Hast du eventuell versäumt, ein Bild des Brunnens zu posten?

 

2)

Zunächst eine Skizze:

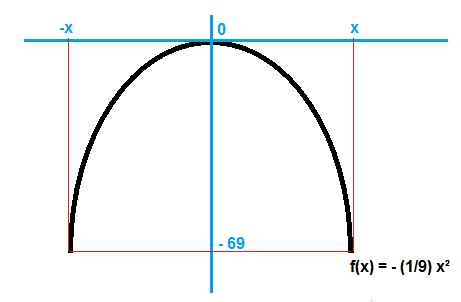
Der Brückenbogen is in Schwarz dargestellt, das Koordinatensystem in Blau.

An den Stellen x und - x muss gelten:

- ( 1 / 9 ) x ² = - 69

Die gesuchte Spannweite W des Brückenbogens ist dann:

W = 2 * x

Also:

- ( 1 / 9 ) x ² = - 69

<=> ( 1 / 9 ) x ² =  69

<=> x ² = 9 * 69 = 621

<=> x ≈ ± 24,92 m

Somit beträgt die Spannweite W etwa

W = 2 * x = 2 * 24,92 = 49,84 m

 

3)

Geht man davon aus, dass der Körperschwerpunkt im Moment der Landung dieselbe Höhe hatt wie beim Absprung, dann muss sich der Scheitelpunkt der Flugbahn genau in der Mitte zwischen Absprung- und Landepunkt befinden, also bei

x = 8,90 / 2 = 4,45

Die angegebene Flugbahngleichung

y = - 0,0571 x ² + 0,3838 x + 1,14

liefert für x = 4,45 den Wert

y ≈ 1,72 m

Der Körperschwerpunkt erreicht also während de Fluges eine maximale Höhe von 1,72 m. Das genügt sicher nicht, um einen VW-Golf zu überspringen.