Aufgabe:
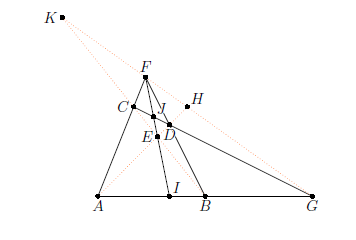
Die in der Abbildung dargestellte Figur heißt vollständiges Viereck. Es besteht aus den Eckpunkten A, B, C, D und sämtlichen Verbindungsgeraden. Die eingezeichneten strichlierten Geraden bilden das sogenannte Diagonaldreieck. Auf diesen Geraden befinden sich jeweils vier Punkte. Zeichnen Sie die Figur in Geogebra und bestimmen Sie deren Doppelverhältnisse sowohl in GeoGebra als auch rechnerisch.
Hinweis: Durch eine projektive Transformation können Sie das Viereck ABCD in ein Viereck mit besonders einfachen Koordinaten überführen.
Problem/Ansatz:
Mit Geogebra ist die Aufgabe kein Probelm, aber ich weiß nicht wie ich durch projektive Transformation auf die Kordinaten kommen soll.
Der Punkt I soll zum Beispiel so definiert sein: I = A + \( \frac{2}{3} \)B
aber wie komme ich auf die \( \frac{2}{3} \)?