In einer Urne sind 1 blaue 4 gelbe und 5 rote Kugeln. Es werden zufällig 10 Kugeln nacheinander mit zurücklegen aus der Urne gezogen.
Bestimme die Wahrscheinlichkeit.: Es werden genau 3 rote Kugeln gezogen
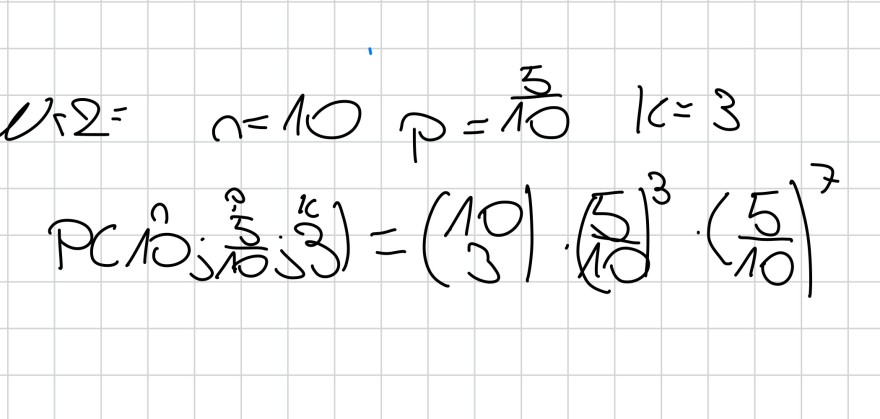
Stimmt das so ganz ohne die Lösung also nur der Weg