Hallo,
Wichtig, Du mußt Eure Definitionen in der Vorlesung benutzen, dies ist nur ein möglicher Weg.
1.Umwandlung in ein DGL -System 1.Ordnung
Setze:
x= z1
x'=z2
\( \begin{aligned} z_{1}^{\prime}= & x^{\prime}=z_{2}, \\ & x^{\prime \prime}=z_{2}^{\prime} \\ \Rightarrow \quad z_{1}^{\prime}= & z_{2} \\ z_{2}^{\prime}= & z_{1}-2 z_{1}^{3}\end{aligned} \)
2. Gleichgewichtspunkte bestimmen , z1' und z2' =0 setzen
ich habe erhalten:
\( (z1, z2)=(0,0),\left(\frac{1}{\sqrt{2}}, 0\right),\left(-\frac{1}{\sqrt{2}}, 0\right) \)
3. Jacobi Matrix aufstellen:
\( J=\left(\begin{array}{cc}0 & 1 \\ 1-6 z_{1}^{2} & 0\end{array}\right) \)
4.Gleichgewichtspunkte in die Jacobi Matrix einsetzen
5.Stabilität/Instabilität bestimmen
Gemäß Punkt 2 Ergebnisse von links nach rechts:

stabil weil ,Eigenwerte auf der imag. Achse
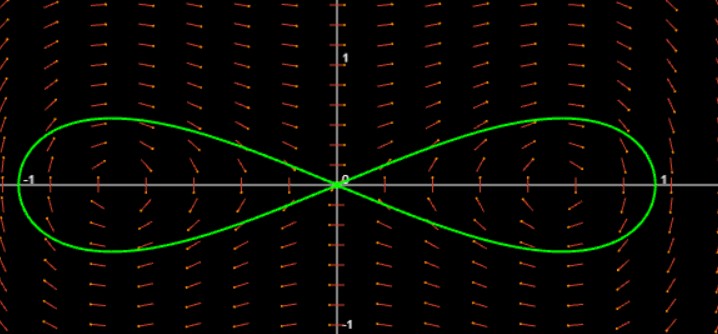
6. Phasenportrait zeichnen (mittels Punkte 2 bis 5)
Wolfram Alpha:
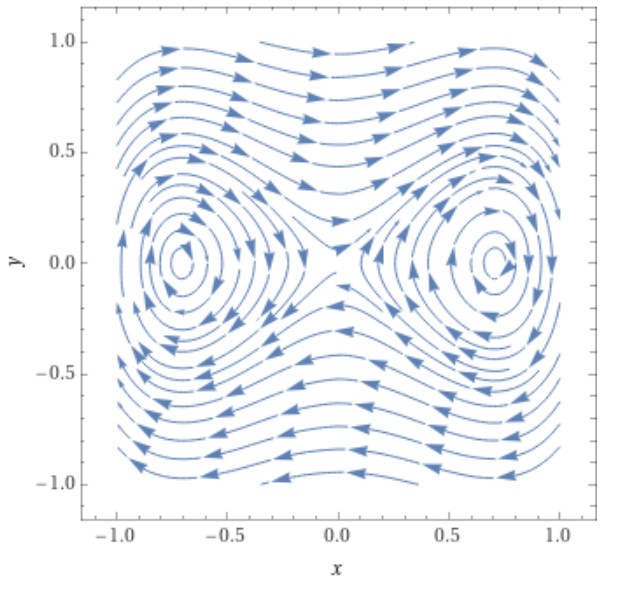
oder: