Wo und unter welchen Winkeln schneidet der Graph von f(x) die Koordinatenachsen?

Question

Hey,

Ich habe die Aufgabe als Bild im Anhang.

Diese befindet sich in einer Übungsserie für eine Arbeit der Differentialrechnung. Ich verstehe zwar, wie ich auf die Schnittstellen mit der x-Achse komme, aber kann nicht nachvollziehen, woher die 4.2 , -2.4 ,.. kommen. Ich benutze einen TR Casio fx-7400gi - Eventuell könnte mir da jemand die Vorgehensweise zusätzlich erklären.

Dankesehr!

Text erkannt:

c) Wo und unter welchen Winkeln schneidet der Graph von \( f(x) \) die Koordinatenachsen?

Schnittwinkel mit der x-Achse:
Nullstellen: \( \quad \mathrm{x}_{0_{1}}=-4 \quad \mathrm{x}_{0_{2}}=-1 \quad \mathrm{x}_{0_{3}}=3 \)
\( \begin{array}{l} \mathrm{f}^{\prime}\left(\mathrm{x}_{0_{1}}=-4\right)=4,2=\tan \gamma \rightarrow \gamma=76,6^{\circ} \\ \mathrm{f}^{\prime}\left(\mathrm{x}_{0_{2}}=-1\right)=-2,4=\tan \delta \rightarrow \delta=-67,4^{\circ} \\ \mathrm{f}^{\prime}\left(\mathrm{x}_{0_{3}}=3\right)=5,6=\tan \varepsilon \rightarrow \varepsilon=79,9^{\circ} \end{array} \)

Comments

tan(x) = 4,2

x= 1,33 Winkel im Bogenmaß

Umrechnung ins Gradmaß:

x/pi=γ/180°

γ = 76,6°

---

Danke für den Kommentar. Ich verstehe leider immer noch nicht, wie wir auf die 4.2 kommen?

tan (x) ist das tan (-4) ? Sorry.

Answer 1

Deine Funktion lautet vermutlich ausmultipliziert

f(x) = 0.2·x^3 + 0.4·x^2 - 2.2·x - 2.4

und die Ableitung daher

f'(x) = 0.6·x^2 + 0.8·x - 2.2

Setze jetzt in die Ableitung für x die Werte -4, -1 und 3 ein. Du solltest deine gewünschten Werte erhalten.

Answer 2

Die Rechnung steht doch quasi da. Setze die Schnittstellen mit der \(x \)-Achse in die erste Ableitung ein.

Ist nicht klar, was die Schreibweise \(f'(x_0=-4) \) bedeutet?

Da uns die Funktion nicht bekannt ist, können wir auch nicht mehr dazu sagen. Aber wie gesagt, es ist nur einsetzen und ausrechnen.

Für die Steigung und den Winkel gilt dann der Zusammenhang \( m=\tan(\gamma) \).

Comments

Ich verstehe es noch immer nicht. :/

Wir haben die I. Ableitung: f(x) = 0.6x^2+0.8x-2.2 - Da rein soll ich jetzt die gegebenen Schnittstellen einsetzen und ausrechnen? Also 0.6 mal -4 hoch 2 + 0.8 mal -4 - 2.2 ???

---

So ist es. Beachte, dass man beim Einsetzen von negativen Zahlen, vor allem, wenn man potenziert, Klammern setzt, denn

\((-4)^2\) ist etwas anderes als \(-4^2\).

Das könnte erklären, warum du nicht dieselben Ergebnisse erhältst.

---

Vielen lieben Dank, jetzt hat's Klick gemacht.

---

Das freut mich. Wie gesagt, bei negativen Zahlen muss man immer vorsichtig sein. Lieber eine Klammer zu viel als zu wenig.

Answer 3

Nullstellen:

\( \quad \mathrm{x}_{0_{1}}=-4 \quad \mathrm{x}_{0_{2}}=-1 \quad \mathrm{x}_{0_{3}}=3 \)

\(f(x)=a(x+4)(x+1)(x-3)\)

\(f'(x)\\=a[(x+1)(x-3)+(x+4)(x-3)+(x+4)(x+1)\)

\(f'(-4)=\\a[(-4+1)(-4-3)+(-4+4)(-4-3)+(-4+4)(-4+1)\)

\(f'(-4)=a\cdot 21=4,2\)

\(a\cdot 21=4,2\)

\(a= \frac{4,2}{21}=0,2 \)

\(f(x)=0,2(x+4)(x+1)(x-3)\)

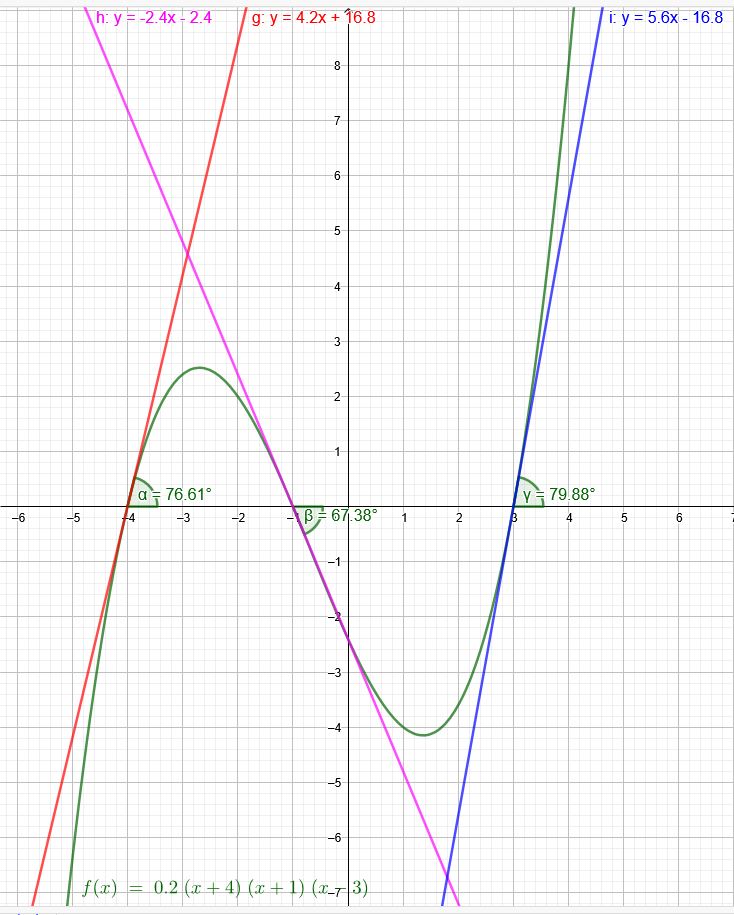
Die Gerade durch N_1((-4|0)\) hat die Steigung \(m_1=4,2\)

Winkelberechnung:

\( \tan^{-1}(4,2)=76,61° \)

Die Gerade durch N_2\((-1|0)\) hat die Steigung \(m_2=-2,4\)

\( \tan^{-1}(-2,4)=180°-67,38°=112,62° \)

Die Gerade durch N_3\((3|0)\) hat die Steigung \(m_3=5,6\)

\( \tan^{-1}(5,6)=79,88° \)