Berechne die Koordinaten der Bildpunkte.

Question

Gegeben ist das Dreieck ABC mit \( \mathrm{A}(1,5 \mid 1), \mathrm{B}(6 \mid 2) \) und \( \mathrm{C}(3 \mid 3) \).

a) Zeichne das Dreieck in ein Koordinatensystem. Bilde es durch Parallelverschiebung mit \( \vec{v}=\binom{-2}{1} \) auf das Dreieck \( A^{\prime} B^{\prime} C^{\prime} \) ab. Berechne die Koordinaten der Bildpunkte.
b) Verschiebe das Dreieck ABC mit dem Gegenvektor \( \overrightarrow{\mathrm{v}^{*}} \) auf das Dreieck \( \mathrm{A}^{*} \mathrm{~B}^{*} \mathrm{C}^{*} \). Berechne die Koordinaten der Eckpunkte dieses Dreiecks.
c) Berechne die Koordinaten der Pfeile \( \overrightarrow{\mathrm{A}^{*} \mathrm{~A}^{\prime}}, \overrightarrow{\mathrm{B}^{*} \mathrm{~B}^{\prime}} \) und \( \overrightarrow{\mathrm{C}^{*} \mathrm{C}^{\prime}} \). Was stellst du fest?

Wie rechnet man mit wktoren

danke

Comments

Hast du keine Unterlagen dazu? Ansonsten findest du zu den Grundlagen doch bereits sehr viel im Internet. Etwas Eigeninitiative sollte nicht schaden!

Answer 1

A = [1.5, 1]
B = [6, 2]
C = [3, 3]

a)

A' = A + v = [1.5, 1] + [-2, 1] = [- 0.5, 2]
B' = B + v = [6, 2] + [-2, 1] = [4, 3]
C' = C + v = [3, 3] + [-2, 1] = [1, 4]

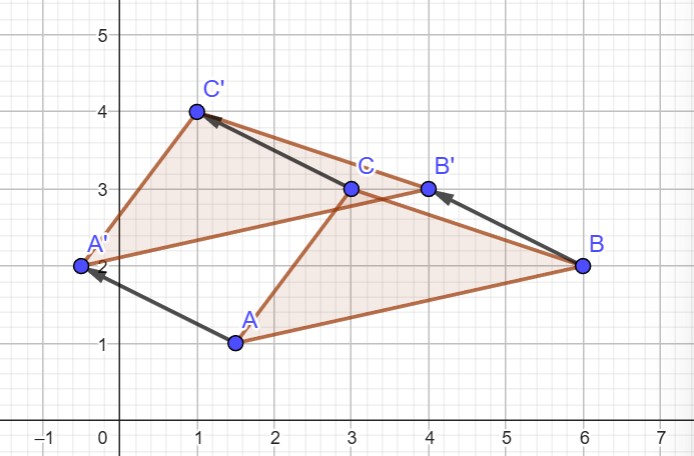
b)

A* = A + v* = [1.5, 1] + [2, -1] = [3.5, 0]
B* = B + v* = [6, 2] + [2, -1] = [8, 1]
C* = C + v* = [3, 3] + [2, -1] = [5, 2]

c)

A*A' = [- 0.5, 2] - [3.5, 0] = [-4, 2]
B*B' = ... = [-4, 2]
C*C' = ... = [-4, 2]

Comments

also ist der anfang richtig

Answer 2

Ortsvektor des Punktes \(B\) ist

        \(\vec{OB} = \begin{pmatrix}6\\2\end{pmatrix}\).

Verschiebung um \(\vec{v}\) ergibt den Ortsvektor

        \(\vec{OB'} = \vec{OB} + \vec{v} = \begin{pmatrix}6\\2\end{pmatrix} + \begin{pmatrix}-2\\1\end{pmatrix} = \begin{pmatrix}6+(-2)\\2+1\end{pmatrix} = \begin{pmatrix}4\\3\end{pmatrix}\)

des Punktes \(B'\).

Der Punkt \(B'\) hat also die Koordinaten \((4|3)\)

Answer 3

Wie rechnet man mit Vektoren?

Beispiel für A(1,5|1) und Parallelverschiebung mit \( \vec{v}=\binom{-2}{1} \):

\( \begin{pmatrix} 1,5\\1 \end{pmatrix} \)+\( \begin{pmatrix} -2\\1 \end{pmatrix} \)=\( \begin{pmatrix} -0.5\\2 \end{pmatrix} \). Dann ist A'(-0,5 | 2).

Comments

danke, das ist sehr nett

---

kannst du mir b und c erklären, was ist ein gegenvektor

---

was ist ein gegenvektor

https://www.google.com/search?q=gegenvektor&oq=gegenvektor&gs_lcrp=EgZjaHJvbWUyBggAEEUYOdIBCDIxNjNqMGo3qAIAsAIA&sourceid=chrome&ie=UTF-8

Ist es so schwierig? Du bemühst dich ja nicht einmal irgendeinen Begriff nachzuschlagen!

---

gehe jemanden anderen nerven

---

Das war nur ein gut gemeinter Rat. Du solltest dich wirklich darum bemühen, etwas mehr Eigeninitiative/Selbstständigkeit zu zeigen. Das wird dir auch in deinem späteren Leben und vielen Bereichen immer wieder helfen, da es nicht immer jemanden geben wird, der dir alles vorkauen wird und kann. Daher sollte man so etwas früh genug lernen.

Und etwas mehr Respekt bitte. Immerhin bekommst du hier kostenfrei deine Aufgaben gemacht. ;)