Question

Warum ist bei der e^x + 2 der Y-Achsenabschnitt bei 3 obwohl der Absolutglied bei 2 ist?

Answer 1

Die Regel mit dem Absolutglied gilt nur bei Polynomfunktionen. Bei allen anderen muss man x=0 einsetzen um möglicherweise eine Regel zu erhalten.

Comments

Wenn ich jetzt e^x - 2 habe, muss ich dann e^-2 einsetzen um den Y-Achsenabschnitt zu bestimmen, also im dem Fall ca. 0,14?

---

MatheNoob, du musst grundsätzlich x=0 einsetzen, um den y- Achsenabschnitt zu erhalten.

---

Und e funktionen haben nie einen Schnittpunkt mit der x-Achse oder sie nähern sich nur dran?

---

Richtig. Reine Exponentialfunktionen der Form

f(x) = a^x mit a > 0 und a ≠ 1

haben die Wertemenge R+. Nehmen also nie den Wert 0 oder negative Werte an.

In der Schule bezeichnet man aber auch

f(x) = e^x - 1

üblicherweise als Exponentialfunktion und so können diese auch den Wert 0 annehmen.

---

Übrigens gilt es bei Polynomfunktionen auch nur in allgemeiner Form und nicht in der Scheitelpunkt oder Faktorisierter Form.

f1(x) = (x - 1)^2 + 2
hat auch den y-Achsenabschnitt 3.

f2(x) = 1/2·(x - 2)·(x - 3)
hat auch den y-Achsenabschnitt 3.

---

Deswegen ist es didaktisch auch sehr schlecht, zu sagen, man könnte den \(y\)-Achsenabschnitt stets ablesen. Leider ist nur den wenigsten wirklich bewusst, dass man ihn mit \(f(0)\) sehr leicht bestimmen kann. Viel mehr sollte man dann verstehen, wann man ihn direkt ablesen kann. Auch hier zeigt sich wieder gut, das Verständnis wesentlich ist im Vergleich zu stumpfer Auswendiglernerei.

Übrigens hat \(f(x)=\sin(x)+c\) den \(y\)-Achsenabschnitt c und es ist keine Polynomfunktion. ;) Ablesen kann ich ihn aber trotzdem, denn \(f(0)=\sin(0)+c=0+c=c\).

---

Text erkannt:

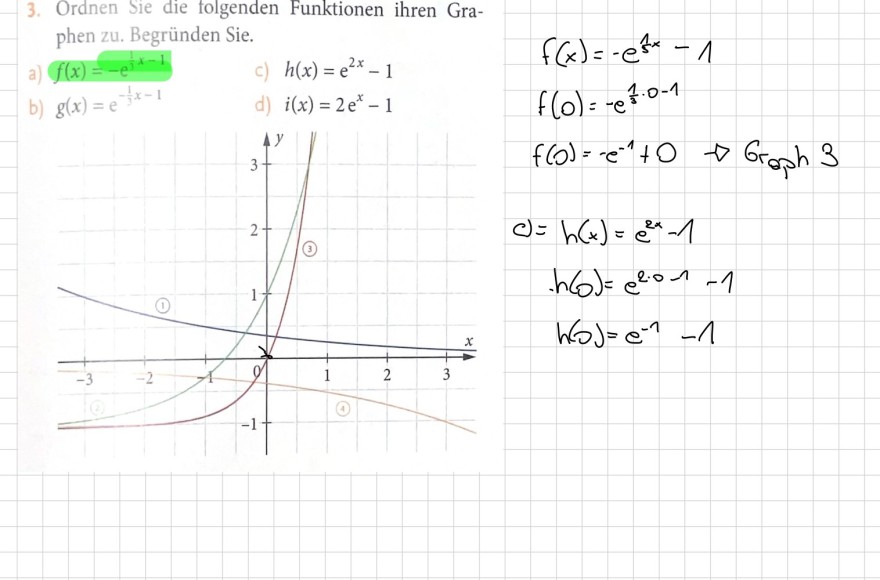
3. Ordnen Sie die folgenden Funktionen ihren Graphen zu. Begründen Sie.
a) \( f(x)=-e^{\frac{1}{3} x-1} \)
c) \( h(x)=\mathrm{e}^{2 x}-1 \)
b) \( g(x)=e^{-\frac{1}{3} x-1} \)
d) \( i(x)=2 \mathrm{e}^{x}-1 \)
\( \begin{array}{l} f(x)=-e^{\tilde{5}^{x}}-1 \\ f(0)=-e^{\frac{1}{3} \cdot 0-1} \\ f(0)=-e^{-1}+0 \rightarrow G_{r_{\text {oph }}} 3 \end{array} \)
\( \begin{aligned} c)= & h(x)=e^{2 x}-1 \\ h(0) & =e^{2 \cdot 0-1}-1 \\ h(0) & =e^{-1}-1 \end{aligned} \)

Wenn man jetzt aber nur Anhand von Berechnung des Schnittpunktes mit der Y—Achse die jeweilige Gleichung zuordnen will, bei der Funktion h(x ) wie macht man das ich habe es versucht aber nicht verstanden, aber am besten nicht wie döschwo erklären sondern bissel besser, wenn es geht.

h(0)= e^2*0-1  -1

h(0)= e^-1 -1

Ich habe da bestimmt was falsch gemacht oder?

---

Ich habe da bestimmt was falsch gemacht oder?

Deine Funktion stimmt gar nicht mit der Funktion der Aufgabe überein. Schau richtig hin. Es gibt hier nichts, was man "besser" erklären kann, da bereits alles gesagt wurde.

---

c) h(x)=e^2x-1; für x=0 ist dann h(0)=e⁰-1=1-1=0. h(0)=0 ist der y-Achsenabschnitt.

Answer 2

Warum ist e⁰ + 2 = 3?

Weil 1 + 2 = 3.