Aufgabe:
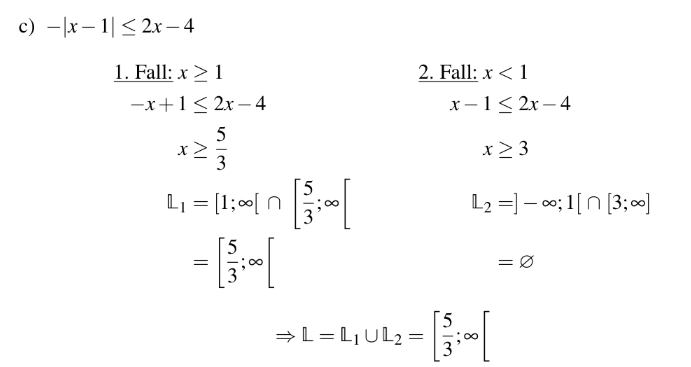
Text erkannt:
c) \( -|x-1| \leq 2 x-4 \)
1. Fall: \( x \geq 1 \)
\( -x+1 \leq 2 x-4 \)
\( x \geq \frac{5}{3} \)
\( \mathbb{L}_{1}=\left[1 ; \infty\left[\cap\left[\frac{5}{3} ; \infty[\right.\right.\right. \) \( =\left[\frac{5}{3} ; \infty[\right. \)
\( \Rightarrow \mathbb{L}=\mathbb{L}_{1} \cup \mathbb{L}_{2}=\left[\frac{5}{3} ; \infty[\right. \)
\( x-1 \leq 2 x-4 \)
\( x \geq 3 \)
\( \left.\mathbb{L}_{2}=\right]-\infty ; 1[\cap[3 ; \infty] \)
\( =\varnothing \)
Kann mir jemand erklären wie man auf den Teil bei Fall 2 kommt?