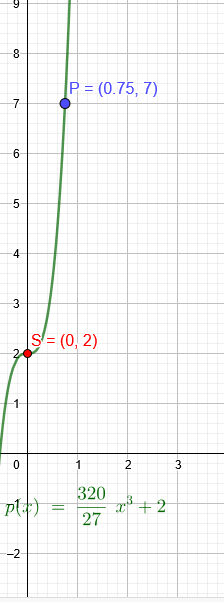
"Ihren y-Achsenabschnitt hat die Funktion bei y=2. Außerdem hat sie an dieser Stelle einen Sattelpunkt. Ein weiterer Punkt liegt bei (3/4, 7)."
Sattelpunkt \(S(0|2)→S´(0|0)\) dreifache Nullstelle:
\(f(x)=a*x^3\)
\(P(\frac{3}{4}| 7)\)→\(P´(\frac{3}{4}| 5)\)
\(f(\frac{3}{4})=a*\frac{27}{64}\)
\(a*\frac{27}{64}=5\) \(a=\frac{320}{27}\)
\(f(x)=\frac{320}{27}*x^3\)
\(p(x)=\frac{320}{27}*x^3+2\)