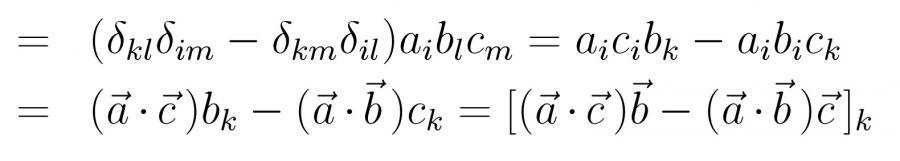Vom Duplikat:
Titel: Bac-cab-Regel beweisen mit Hilfe des Civita-Tensors?
Stichworte: beweis,tensoren,grassmann,regel
Grassmann Identität beweisen?
WAS PASSIERT HIER?.... Man soll die Grassmann regel auch bac minus cab regel gennant, herleiten, mithilfe des levi civita tensors .... Bis zum aller ersten Ausdruck im Bild, komme ich auch... aber dann verstehe ich den naechsten schritt nicht.