Sechseckiges Prisma: Dicke berechnen. Wie viele Liter dieser Versiegelung wurden benötigt?

Question

Das Autohaus Flott erhält zu Werbezwecken ein Kunstobjekt in Form eines sechseckigen Prismas mit einer wetterfesten Nanoversiegelung.

Die Nanoversiegelung wurde 0,5 mm dick aufgetragen. Wie viele Liter dieser Versiegelung wurden benötigt?

Answer 1

Berechne zunächst das Volumen des  Körpers ohne Schutzschicht und dann das Volumen des Körpers mit Schutzschicht. Die Differenz der beiden Volumina ergibt dann das Volumen der Schutzschicht.

a ) Ohne Schutzschicht:

Der Körper ist ein Prisma, also muss zunächst der Flächeninhalt der von den Seiten a und c begrenzten Grundfläche berechnet werden. Durch Multiplikation mit der Höhe b erhält man dann das Volumen. 

b ) Mit Schutzschicht:

Auch nach dem Auftragen der Schutzschicht ist der dadurch enstandene Körper weiterhin ein Prisma. Allerdings sind alle seine Seiten um jeweils 1 mm = 0,001 m länger geworden ( jeweils um 0,5 mm in beide Richtungen). Mit diesen neuen Abmessungen berechnet man nun wie unter a) das Volumen des neuen Körpers.

Davon subtrahiert man das in a) berechnete Volumen und die Differenz ist das Volumen der Schutzschicht.

Achte auf die Einheiten ( m bzw. mm ) und vergiss nicht, das Volumen zum Schluss in Liter umzurechnen.

 

EDIT:

Hier die versprochene Berechnung.

Zunächst eine Skizze:

 

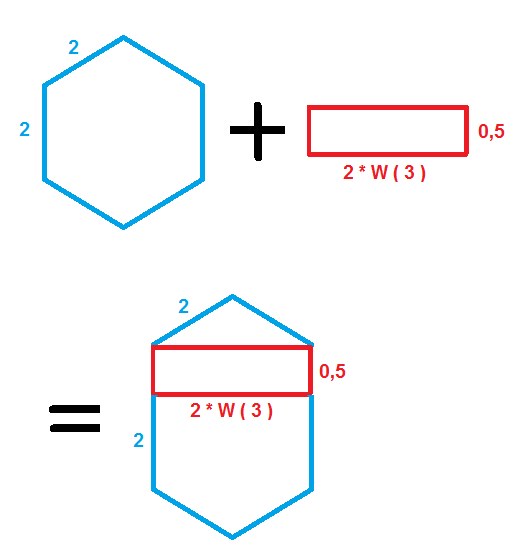
Bei dem Sechseck handelt es sich um ein regelmäßiges Sechseck ( blau ) mit der Seitenlänge a = 2 m , in welches ein Rechteck (rot) der Höhe h_R = c - a = 0,5 m eingesetzt wurde.

Die Breite des Rechtecks ist die Länge der Diagonale über 2 Seiten eines regelmäßigen Sechsecks der Seitenlänge a . Diese kann entweder einer Formelsammlung entnommen werden oder mittels trigonometrischer Betrachtungen berechnet werden. Diese kann ich, falls gewünscht, noch nachliefern.

Formelsammlung bzw. Berechnung ergeben mit der Seitenlänge a des regelmäßigen Sechsecks für die Breite b_R des Rechtecks:

b_R = a * √ ( 3 )

so dass sein Flächeninhalt A_Ralso

A_R = h_R * b_R  = ( c - a ) * a * √ ( 3 )

beträgt.

 

Der Flächeninhalt A_Seines regelmäßigen Sechsecks mit de Seitenlänge a beträgt (Formelsammlung):

A_S = a ² * ( 3 / 2 ) * √ ( 3 )

Damit ergibt sich der Flächeninhalt A_G der Grundfläche des betrachteten Werbeobjektes zu:

A_G = A_R + A_S

= ( c - a )  * a * √ ( 3 ) + a ² * ( 3 / 2 ) * √ ( 3 )

= a * √ ( 3 ) * ( ( c - a ) + ( 3 a / 2 ) ) 

Multipliziert man dies noch mit der Höhe b des Werbeobjektes, dann ergibt sich somit dessen Volumen zu

V = b * A_G = b * a * √ ( 3 ) * ( ( c - a ) + ( 3 a / 2 ) )

Mit den Werten a = 2 m, b = 2 m und c = 2,5 m ergibt sich daraus das Volumen:

V = 2 * 2 * √ ( 3 ) * ( ( 2,5 - 2 ) + ( 3 * 2  / 2 ) )

= 4 * √ ( 3 ) * 3,5

= 14 * √ ( 3 ) m ³

 

Durch das Besprühen mit der Schutzschicht erhöhen sich die Seitenlängen um jeweils 1 mm = 0,001 m, sodass nun also gilt:

a ' = 2,001 m
b ' = 2,001 m
c ' = 2,501 m

Damit ergibt sich das Volumen V ' des besprühten Körpers zu

V ' = b ' * a '  * √ ( 3 ) * ( ( c ' - a ' ) + ( 3 a '  / 2 ) )

= 2,001 * 2,001 * √ ( 3 ) * ( ( 2,501 - 2,001 ) + ( 3 * 2,001  / 2 ) )

= 4,004001 * 3,5015 * √ ( 3 )

= 14,0200095015 * √ ( 3 )

 

Als Differenz, und somit als Volumen V_S der Schutzschicht ergibt sich daraus:

V_S = V ' - V

= 14,0200095015 * √ ( 3 ) - 14 * √ ( 3 )

= 0,0200095015 * √ ( 3 )

≈ 0,034657 m ³

Wegen 1 m ³ = 1000 Liter sind das also etwa 34,657 Liter.

Es werden also 34,657 Liter der Schutzschicht benötigt.