Bevor ich die 15 Werte eingesetzt habe, habe ich die 1. Formel gefunden. Muss man alle Messwerte addieren und durch 15 teilen oder muss man anders rechnen?
zu b)
Umso mehr Messungen gemacht werden, umso geringer ist der Standardfehler.
100%
-99%
<1%
Mindestens 99 Messungen müssen gemacht werden... aber ich denke die Aufgabe wäre dann zu einfach. Es muss also einen anderen Weg geben.
Ich habe die Formeln gefunden!
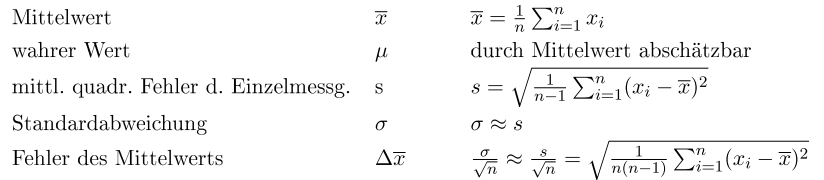
Mal sehen, ob ich die korrekten Lösungen finde.
Ist n die Anzahl der Ergebnisse der Messreihen?
So, wie es jetzt aussieht:
\( \bar{x}=\frac{1}{n} \sum \limits_{i=1}^{n} x_{i} \)
\( \bar{x}=\frac{1}{15} \sum \limits_{i=1}^{15} x_{1}+x_{2}+x_{3}+x_{4}+x_{5}+x_{6}+x_{7}+x_{87} x_{9}+x_{10}+x_{11}+x_{12}+x_{13+} x_{14}+x_{15} \)
\( \bar{x}=\frac{1}{15} * 252,91 \)
\( \bar{x}=16,89067 \)
\( s=\sqrt{\frac{1}{n-1} \sum \limits_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \)
\( s=\sqrt{\frac{1}{15-1} \sum \limits_{i=1}^{15}(252,91-16,89067)^{2}} \)
\( s=\sqrt{\frac{1}{14} *(252,91-16,89067)^{2}} \)
\( s=-2,24 \)
Unter dem Wurzelbetrag sind Minusergbnisse, also nicht lösbar?
\( \bar{x}=\frac{I}{n} \sum \limits_{i=1}^{n} x_{i} \)
\( \bar{x}=\frac{1}{15} \sum \limits_{i=1}^{15} x_{i}+x_{2}+x_{3}+x_{4}+x_{5}+x_{6}+x_{7}+x_{8} x_{9}+x_{10}+x_{1 i}+x_{12}+x_{13+} x_{14}+x_{15} \)
\( \bar{x}=\frac{1}{15} * 252,91 \)
\( \bar{x}=16,89067 \)
\( s=\sqrt{\frac{1}{n-1} \sum \limits_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \)
\( s=\sqrt{\frac{1}{15-1} \sum \limits_{i=1}^{15}(252,91-16,89067)^{2}} \)
\( s=\sqrt{\frac{1}{14} *(252,91-16,89067)^{2}} \)
\( s=\sqrt{-2,24} \)
\( \frac{\sigma}{\sqrt{n}} \approx \frac{\sigma}{\sqrt{s}}=\sqrt{\frac{1}{n(n-1)} \sum \limits_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \)
\( \frac{\sigma}{\sqrt{n}} \approx \frac{\sigma}{\sqrt{s}}==\sqrt{\frac{1}{15(15-1)} \sum \limits_{i=1}^{15}(252,91-16,89067)^{2}} \)
\( \frac{\sigma}{\sqrt{n}} \approx \frac{\sigma}{\sqrt{s}}==\sqrt{\frac{1}{210} *(252,91-16,89067)^{2}} \)
\( \frac{\sigma}{\sqrt{n}} \approx \frac{\sigma}{\sqrt{s}}==\sqrt{-0,149} \)
Ich vermute, dass die Lösungen falsch sind, denn da es sich nicht um komplexe Zahlen handelt, darf unter einer Wurzel kein Minusbetrag stehen. Es kann sein, dass die Forumuser unsicher sind, aber ihr könnt zumindest überprüfen, ob die Zahlen in den Formeln richtig eingesetzt sind. Vielleicht hätte ich für n einen anderen Wert nehmen müssen.
Erster Wert muss richtig sein, die Wurzelergebnisse nicht...
Vielleicht hilft es, wenn wir es Schritt für Schritt machen:
1.) Was setze ich für n ein?
2.) Was setze ich für xi ein?
3.) Was kommt für -x- raus?