Kurvendiskussion bei dieser Funktion: x^3/(x^2-1)

Question

f(x)= x³/(x²-1) 

(1) Definitionsbereich

(2) Symmetrie

(3) Verhalten für x →∞ und für x →-∞

(4) Verhalten der Funktionswerte in der Nähe der Definitionslücken

(5) Extrempunkte

(6) Wendepunkte

(7) Wertemenge

(8) Zeichne den Graphen von f

 

Ich könnte eigentlich Extrema und Wendepunkte und Symmetrie und Definitionsbereich  berechnen...aber kann das mal einer komplett berechnen? Besondern wichtig diese Verhalten.....

Ableiten würde man das doch mit der Quotientenregel machen oder?

Answer 1

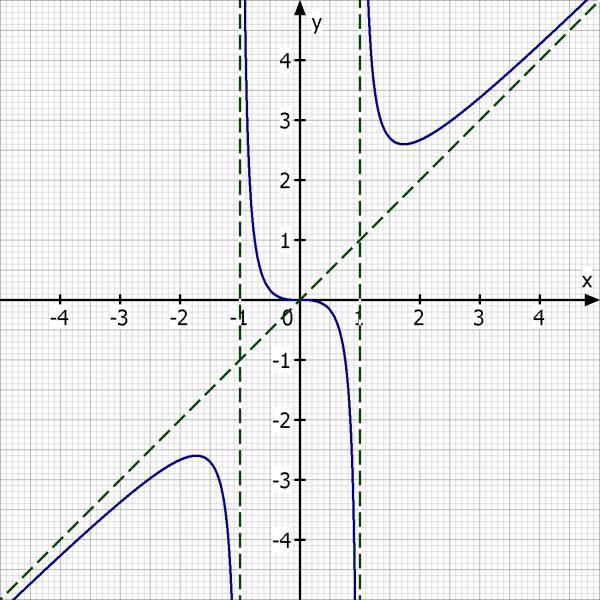
Funktion und Ableitungen

f(x) = x^3/(x^2 - 1)
f'(x) = (x^4 - 3·x^2)/(x^2 - 1)^2
f''(x) = (2·x^3 + 6·x)/(x^2 - 1)^3

Definitionsbereich

x^2 - 1 = 0
x = ±1
D = R \ {±1}

Symmetrie

Im Zähler steht eine Ungerade Funktion und im Nenner eine gerade Funktion. Damit haben wir eine ungerade Funktion die Punktsymmetrisch ist.

Verhalten für x → ∞ und für x → -∞

f(x) = x^3/(x^2 - 1) = x + x/(x^2 - 1)

y = x ist eine schräge Asymptote an die sich der Graph annähert.

lim (x → ∞) = ∞
lim (x → -∞) = -∞

Verhalten der Funktionswerte in der Nähe der Definitionslücken

lim (x → -1-) = -∞
lim (x → -1+) = ∞
lim (x → 1-) = -∞
lim (x → 1+) = ∞

Extrempunkte f'(t) = 0

x^4 - 3·x^2 = 0
x = 0 oder x = ± √3

f(0) = 0 --> Wendepunkt siehe nächster Teil
f(- √3) = - 3/2·√3 --> HP(-1.73 | -2.60)
f(√3) = 3/2·√3 --> TP(1.73 | 2.60)

Wendepunkte f''(t) = 0

2·x^3 + 6·x = 0

x = 0

f(0) = 0 --> Einziger Wendepunkt

Wertemenge

W = R

Zeichne den Graphen von f

 

Comments

Hallo Mathecoach :)

wow Super

Allerdings verstehe ich die Sachen mit den Grenzwerten nicht, also mit den Verhalten im Unendlichen :(

PS: Hab ich dir schon gesagt, dass ich in der Mathe Arbeit (Trigonometrie) 2+ geschrieben habe? :(

Mir haben 0.5P zur 1 gefehlt :(

---

Herzlichen Glückwunsch zur 2+

Das mit den Grenzwerten ist so etwas schlecht zu erklären. Ich mache das über die Vorzeichenwechsel im Zähler und Nenner. Du kannst ganz unprofessionell folgende Funktionswerte bestimmen

f(-1.1)

f(-0.9)

f(0.9)

f(1.1)

Dann hast du schon eine Ahnung wo die Grenzwerte hingehen. Ansonsten muss ich dazu mal ein Video machen um die das mit den Vorzeichenwechseln besser zu erklären.

---

Danke :)

Ich muss jetzt sowieso schlafen :)

Und ja ein Video wäre suuuuuuuuuuppppeeerrr...du erklärst das einfach so gut :) (Hier natürlich auch, aber beim Video ist es doch irgendwie anders) :)

:)

---

@Der_Mathecoach: Wie viel Zeit hast du in etwa für die Erstellung, das Speichern und das Hochladen des Graphenbildes benötigt?

Hier habe ich zur Eingabe per internem Grapheinbetten unter 30 Sekunden gebraucht:

~plot~ x^3/(x^2-1);x=-1;x=1;x ~plot~

Bin im Test- bzw. Vergleichsmodus, was den Zeitaufwand betrifft, danke.

---

Ich habe sicher 4 mal so lange gebraucht. Dafür aber auch die Farben frei wählen können und Asyptote und Geraden gestrichelt zeichnen können. Aber ich werde sicher auch bald auf den internen Graphenplotter umsteigen. 

---

Grundsätzlich sind alle Features möglich, die auch hier zu finden sind: http://fooplot.com/ Der dortige Plotter ist derselbe, den wir verwenden.

Es ist nur nicht einfach, sich die entsprechende Syntax auszudenken. 

Zum Beispiel überlege ich noch - hatte ich bei einer Antwort von dir gesehen -, dass der sichtbare Koordinatenbereich selbst festgelegt werden kann. Zum Beispiel: -10 < x < 10 und -20 < y < 20. Heute habe ich mir als Syntax [[ 10|10|-20|20 ]] überlegt [[ xmin, xmax, ymin, ymax]].

Mit zunehmenden Features kommt immer mehr Syntax hinzu und es wird komplexer :) Wahrscheinlich wird es daher Farbwahl und gestrichelte Linien nicht geben. Die Zusatzsyntax/Lernaufwand steht nicht im Verhältnis zum Mehrwert.

---

Das Festlegen des Koordinatenbereichs wurde soeben eingebaut, hier ein Beispiel: 

~plot~ 2*x;x^4-2x^3;{1|2};x=1;[[-2|3|-2|5]] ~plot~

Das ist ein schönes Feature, um selbst zu "zoomen" =)

---

ich hätte bezüglich dieser Aufgabe noch eine Frage zum  Monotomieverhalten. Ich habe für das Intervall Wurzel 3 bis Unendlich monoton wachsend heraus und für das Intervall 1 bis Wurzel 3 monoton fallend. Jedoch habe ich dieses im Internet überprüft und dort ist es umgekehrt. Kann mir jemand weiterhelfen? :)

---

Monoton steigend

f'(x) >= 0

(x^4 - 3·x^2)/(x^2 - 1)^2 >= 0

Der Nenner ist eh positiv damit braucht man nur den Zähler untersuchen

(x^4 - 3·x^2) >= 0

x^2·(x^2 - 3) >= 0

Auch x^2 ist immer positiv

x^2 - 3 >= 0 --> x ≤ - √3 ∨ x ≥ √3

monoton steigend für x ≤ - √3 oder x ≥ √3

In den anderen Bereichen also streng monoton fallend.

---

danke für die schnelle verständliche Antwort, daher wundere ich mich auch wieso der Rechner dieses raus hat:http://matheguru.com/rechner/kurvendiskussion/

---

Da hat der Rechner von Matheguru wohl einen Fehler wie man unschwer am Graphen selber erkennen kann. Das ist aber nichts außergewöhnliches. Es wurden in dem Rechner bereits mehrere Fehler festgestellt. Da kann man nur hoffen, dass diese irgendwann behoben werden.