Gegeben ist eine Differentialgleichung der Form
\( \frac{\mathrm{d}}{\mathrm{d} t} x=f(x) \)
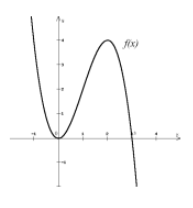
und die rechts abgebildete graphische Darstellung der Funktion \( f(x) \).
(Bsp) Was können Sie über die Ordnung und Linearität der Differentialgleichung schlussfolgern?
(a) Bestimmen Sie aus der Abbildung die stationären Lösungen der Differentialgleichung. Geben Sie an, ob diese stabil oder instabil sind.
(b) Überlegen Sie sich qualitativ, wie die Lösung \( x(t) \) der Differentialgleichung für die drei Anfangsbedingungen \( x(0)=-1 ; x(0)=0,5 \) und \( x(0)=3,5 \) jeweils aussieht (ohne Rechnung!). Fertigen Sie eine Skizze dieser drei speziellen Lösungen an.
(c) Welcher der folgenden Funktionsvorschriften lässt sich die Skizze von \( f(x) \) zuordnen? Woran erkennen Sie es?
\( \begin{array}{l} g(x)=x^{3}-3 x^{2} \\ h(x)=-x^{4}+3 x^{2} \\ j(x)=-x^{3}+3 x^{2} \\ k(x)=x^{4}-3 x^{2} \end{array} \)
(d) Zusatzaufgabe: Versuchen Sie, die Funktionsvorschrift für \( f(x) \) nur anhand der Skizze von \( f(x) \) zu konstruieren. Welche Informationen aus der Skizze sind hierfür wichtig?
eine weitere Aufgabe zu DGL ist gegeben.
Ansatz:
a)
1. Ordnung und linear, da nicht x2 vorhanden.
-∞<0 monoton fallend, instabil
0>3 monoton steigend, stabil
3>∞ monoton fallend, instabil
Insgesamt instabil
zu b)
Könnte man nicht die 3 Anfangsbedingungen nicht in j(x) einsetzen? Ich kann mir vorstellen, dass dieser Ansatz falsch ist, habe aber unten meine Ideen aufgeschrieben:
d/dt x f(x)
x(0)=-1
x(0)=0,5
x(0)=3
j(x)=-x³+3x²
j(-1)=-(-1)³+3(-1)²=2
j(0,5)=-0,5³+3x²=0,625
j(3,5)=-x³+3x²=-42,875+36,75=-6,125
c)
j(x), habe bei Geogebra eingegeben und ist exakt die Funktion, wie auf dem Aufgabenblatt.