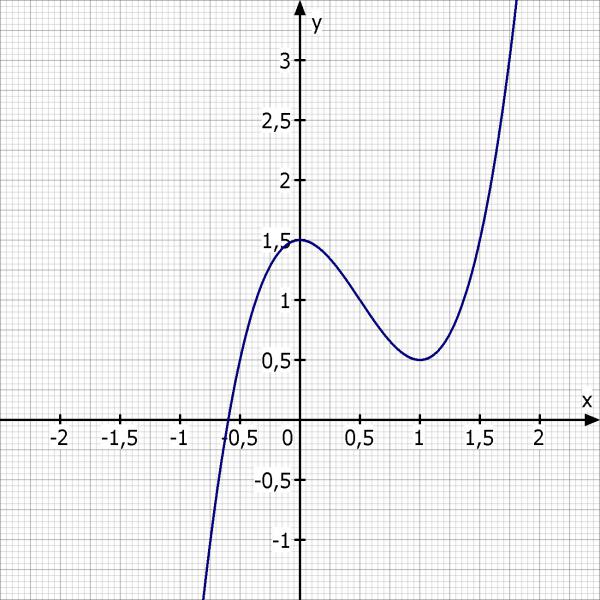
Die gesuchte Funkton 3. Grades
f(x) = a·x^3 + b·x^2 + c·x + d
schneidet die y Achse bei 1,5.
f(0) = 1.5
d = 1.5
Gleichzeitig liegt hier ein Maximum vor.
f'(0) = 0
c = 0
Bei x=0,5 geht die Kurve von einer Rechts - in eine Linkskrümmung über.
f''(0.5) = 0
3·a + 2·b = 0
Bei x=1 ist der zugehörige y-Wert 0,5.
f(1) = 0.5
a + b + 0 + 1.5 = 1/2
Stellen Sie dafür ein Gleichungssystem auf und ermitteln sie die Funktionsgleichung mit dem Gauß´schen Eliminationsverfahren oder dem Additionsverfahren.
3·a + 2·b = 0
a + b = -1
Als lösung ergibt sich: a = 2 ∧ b = -3
Damit haben wir die Funktion
f(x) = 2·x^3 - 3·x^2 + 1.5
Skizze