Also wenn wir die Funktion f mit f(x)=g(x)h(x) ableiten wollen, dann gehen wir folgendermaßen vor :
Wir schreiben den Funktionsterm mithilfe der e-Funktion und der ln-Funktion folgendermaßen um :
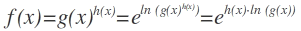
und können jetzt ableiten :
f'(x) = eh(x)·ln (g(x)) ·[h(x)·ln (g(x))]' = eh(x)·ln (g(x))·( h'(x)·ln (g(x)) + h(x)·(1/g(x))·g'(x) ) =
g(x)h(x) ·( h'(x)·ln (g(x)) + h(x)·(1/g(x))·g'(x) )
Wenn du mehrfach geschachtelte Exponenten hast, musst du diese Regel mehrfach anwenden.