Wenn ich es richtig verstanden habe, ist die gegebene Funktion
f ( x ) = 0,5*(4-(4/9)x2)-0,5*(-8/9) x
die Ableitung einer Funktion F ( x ) und du sollst ( oder willst ) die Extremstelle von F ( x ) bestimmen. Dazu hast du die Ableitung f ( x ) gebildet und willst nun deren Nullstelle(n) bestimmen, weil nur dies Extremstellen von F ( x ) sein können.
Ist das richtig?
Nun, f ( x ) kann man auch so schreiben:
f ( x ) = 0,5 * ( 4 - ( 4 / 9 ) x 2 ) - 0,5 * ( - 8 / 9 ) x
= - ( 4 / 9 ) x / √ ( 4 - ( 4 / 9) x 2 )
= - ( 4 / 9 ) x / √ ( ( 36 / 9 ) - ( 4 / 9) x 2 )
= - ( 4 / 9 ) x / √ ( ( 4 / 9 ) * ( 9 - x 2 ) )
= - ( 4 / 9 ) x / ( 2 / 3 ) * √ ( 9 - x 2 ) )
= ( - 2 / 3 ) x / √ ( 9 - x 2 )
= - 2 x / ( 3 √ ( 9 - x 2 ) )
bzw. in TeX:
$$\frac { -2x }{ 3\sqrt { 9-{ x }^{ 2 } } }$$
und das ist mitnichten eine Parabel.
Auch die Stammfunktion F ( x ) von f ( x ) ist keine Parabel, diese habe ich mir mal von WolframAlpha berechnen lassen. Sie lautet:
F ( x ) = ( 2 / 3 ) * √ ( 9 - x 2 )
Die Graphen der Stammfunktion F( x ) und der Ableitung f ( x ) sehen so aus:
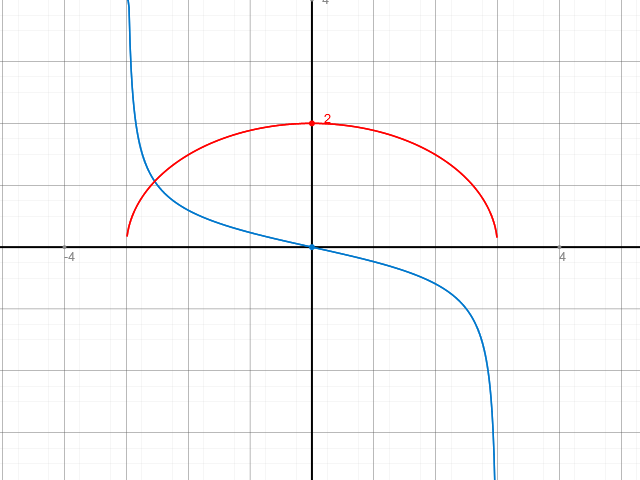
Wie man sieht, hat zwar die Stammfunktion F ( x ) eine Extremstelle, nicht aber die Ableitung f ( x ) .
Um nun die Extremstelle von F ( x ) zu finden muss man die Ableitung f ( x ) gleich Null setzen und nach x auflösen, also:
f ( x ) = - 2 x / ( 3 √ ( 9 - x 2 ) ) = 0
Ein Bruch hat genau dann den Wert 0, wenn sein Zähler den Wert Null hat und sein Nenner einen Wert ungleich Null hat, also
<=> - 2 x = 0 und ( 3 √ ( 9 - x 2 ) ) ≠ 0
<=> x = 0
Und das ist der Kandidat für eine Extremstelle von F ( x ) = ( 2 / 3 ) * √ ( 9 - x 2 )