Fertige zunächst eine Skizze an:
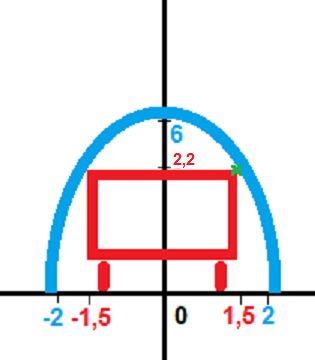
Wenn der Torbogen eine Parabelform hat, muss er sich durch eine Funktionsgleichung der Form
f ( x ) = a x 2 + b x + c
(allgemeine Parabelgleichung) beschreiben lassen.
Nun müssen die Parameter a, b und c so bestimmt werden, dass die Funktion f mit diesen Parameterwerten die Form des Torbogens beschreibt.
Legt man das Koordinatensystem so, dass die Parabel symmetrisch zur y-Achse liegt (siehe Skizze), dann müssen folgende Gleichungen gelten:
Für x = 0 :
f ( 0 ) = a * 0 2 + b * 0 + c = 6
Für x = - 2 :
f ( - 2 ) = a * ( - 2 ) 2 + b * ( - 2 ) + c = 0
Für x = 2 :
f ( 2 ) = a * 2 2 + b * ( - 2 ) + c = 0
Aus der ersten Gleichung folgt sofort:
c = 6
Setzt man dies in die beiden anderen Gleichungen ein, erhält man:
a * ( - 2 ) 2 + b * ( - 2 ) + 6 = 0
a * 2 2 + b * ( - 2 ) + 6 = 0
<=>
4 a - 2 b + 6 = 0
4 a + 2 b + 6 = 0
Additionsverfahren: Zweite Gleichung minus erste Gleichung:
0 a + 4 b + 0 = 0
<=> b = 0
Einsetzen in eine der beiden voranstehenden Gleichungen (ich nehme die erste):
4 a - 2 * 0 + 6 = 0
<=> 4 a = - 6
<=> a = - 3 / 2
Nun hat man die Werte der drei Parameter bestimmt und kann die Funktionsgleichung aufstellen, die den Torbogen beschreibt:
f ( x ) = a x 2 + b x + c = ( - 3 / 2 ) x 2 + 0 x + 6 = ( - 3 / 2 ) x 2 + 6
Das beschriebene Fahrzeug passt genau dann nicht durch den Torbogen, wenn es auch bei optimaler (also mittiger) Durchfahrt mit der in der Skizze grün markierten oberen Fahrzeugecke an dem Torbogen hängenbleiben würde. Das ist dann der Fall, wenn der Torbogen an der Stelle x = 1,5 nicht höher als das Fahrzeug ( Höhe: 2,2 m ) ist, wenn also gilt:
f ( 1,5 ) ≤ 2,2
Ausrechnen (blau gesetzte Funktionsgleichung) :
f ( 1,5 ) = ( - 3 / 2 ) * 1,5 2 + 6 = 2,625
Also: Der Torbogen ist an der Stelle x = 1,5 m 2,625 m hoch und damit höher als das Fahrzeug, sodass dieses den Torbogen also gefahrlos durchfahren kann.