Funktionsscharen? wie genau löst man eine Aufgabe?

Question

Gegeben sind eine Parabel P und die Gerade gk. Die zugehörigen Funktionsterme sind
f(x)= - (x-2)²+3 und gk(x) =kx+3 jeweils mit der Definitionsmenge IR und dem reellen Parameter k für die Gerade gk.
Bestimmen Sie diejenigen Werte k IR, für welche die Gerade gk und die Parabel P genau einen Punkt  gemeinsam haben.

Answer 1

 

um gemeinsame Punkte bzw. einen gemeinsamen Punkt von f(x) und g_k(x) herauszufinden, muss man die beiden Funktionsterme gleichsetzen:

 

- (x - 2)² + 3 = kx + 3 | - 3

- (x - 2)² = kx

- (x² - 4x + 4) = kx | * (-1)

x² - 4x + 4 = -kx | + kx

x² - 4x + kx + 4 = 0

x² - (4 - k) * x + 4 = 0

pq-Formel

x_1,2 = 2 - k/2 ± √((2 - k/2)² - 4)

Wenn der Ausdruck unter der Wurzel = 0 ist, haben wir nur eine Lösung, also nur einen gemeinsamen Punkt, also:

(2 - k/2)² = 4

4 - 2k + k²/4 = 4 | - 4

k²/4 - 2k = 0 | * 4

k² - 8k = 0

k * (k - 8) = 0

Ein Produkt ist dann 0, wenn mindestens einer der Faktoren = 0 ist. Hier also

k₁ = 0

k₂ = 8

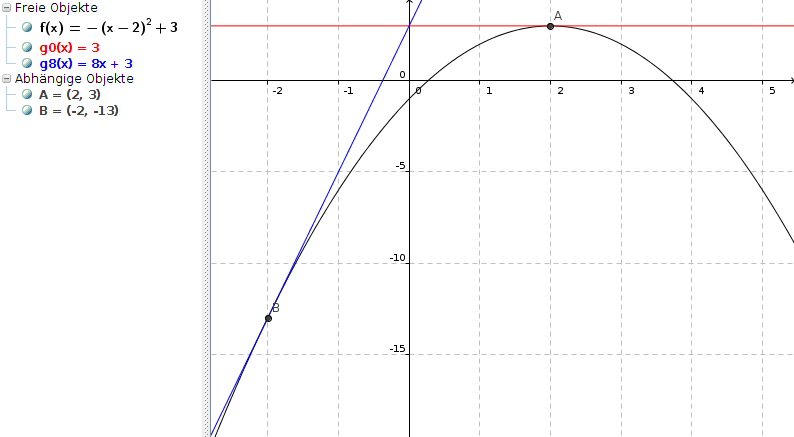
g₀(x) = 0 * x + 3 = 3

g₈(x) = 8x + 3

 

Berührpunkt im 1. Falle:

- (x - 2)² + 3 = 3 | - 3

- (x - 2)² = 0

(x - 2)² = 0

A(2|3)

 

Berührpunkt im 2. Falle:

- (x - 2)² + 3 = 8x + 3 | - 3

- (x - 2)² = 8x | * (-1)

(x - 2)²  = -8x

x² + 4x + 4 = 0

x_1,2 = -2 ± √(4 - 4) = -2

B(-2|f(-2)) = B(-2|-13)

 

 

Besten Gruß

Answer 2

Schnittstelle f(x) = g(x)

- (x - 2)^2 + 3 = k·x + 3
- x^2 + 4·x - 1 = k·x + 3
x^2 + x·(k - 4) + 4 = 0

Diskriminante b^2 - 4·a·c = 0

(k - 4)^2 - 4·(1)·(4) = 0
(k - 4)^2 - 16 = 0
(k - 4)^2 = 16
k - 4 = ± 4
k = 4 ± 4
k = 0 oder k = 8