Funktion Monotonie steigend fallend? Wie berechnet man dies?

Question

wie berechne ich ob eine Funktion monoton fallend / monoton steigend ist?
Beispiel: x^3 - 1

Bitte die Rechnenschritte ausführlich erklären.
Mir ist bekannt, dass wenn x1 < x2 und wenn gilt f(x1)<f(x2) dann ist die Funktion monoton wachsend.

Was ist wenn es nur ein x gibt? sprich x1 = x2 ist? Oder kann das nicht passieren?

Answer 1

 

hast Du schon gelernt, wie man die 1. Ableitung einer Funktion bildet? Wenn ja, dann ist das recht einfach:

 

f(x) = x³ - 1

f'(x) = 3x²

Wenn f'(x) in einem Bereich immer größer als 0 ist, dann ist die Funktion in diesem Bereich streng monoton steigend.

Wenn f'(x) in einem Bereich größer als 0 und irgendwo in diesem Bereich gleich 0 ist, dann ist die Funktion in diesem Bereich monoton steigend.

Umgekehrt:

Wenn f'(x) in einem Bereich immer kleiner als 0 ist, dann ist die Funktion in diesem Bereich streng monoton fallend.

Wenn f'(x) in einem Bereich kleiner als 0 ist und irgendwo in diesem Bereich gleich 0 ist, dann ist die Funktion in diesem Bereich monoton fallend.

 

In Deinem Beispiel sieht man, dass f'(x) im gesamten Bereich der reellen Zahlen größer oder gleich 0 ist (für x = 0 gilt f'(x) = 0). Deshalb ist die Funktion im gesamten Bereich der reellen Zahlen monoton steigend - aber nicht streng monoton steigend, weil f'(0) = 0:

 

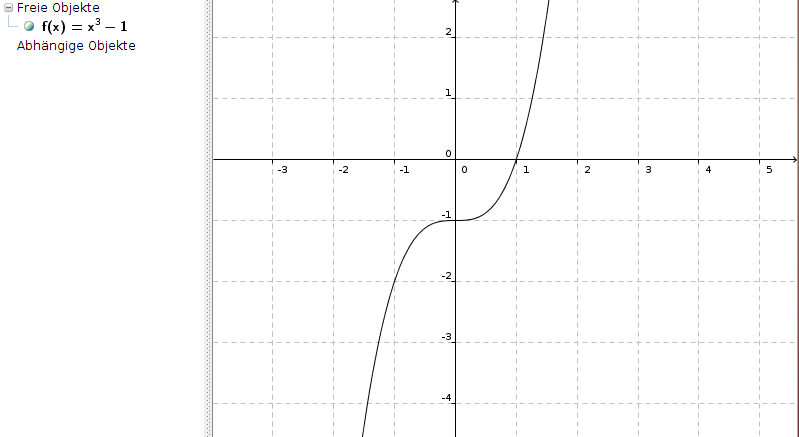
In ℝ\{0} ist sie sogar streng monoton steigend, weil dort f'(x) > 0 für alle x gilt.

Alles klar?

 

Besten Gruß

Answer 2

Hi,

habt Ihr schon Ableitungen gehabt, dann gehts am einfachsten. Mit \( f(x)=x^3-1 \) folgt \( f'(x)=3x^2 \) und das ist immer größer 0, also ist die Funktion monoton wachsend.

Comments

Wenn ich für x = 0 einsetzte wäre es aber nicht größer sondern gleich 0...??

---

Korrekt :-)

Siehe meine Antwort :-D

---

dafür ist die Antwort nicht korrekt

---

Natürlich ist seine Antwort korrekt. die Steigung ist in diesem Punkt also gleich 0. 3*0^3 = 0 eine Funktion ist monoton wachsend wenn die Steigung <=0 ist. Während eine Funktion streng monoton wachsend ist, wenn die Steigung <0 ist, also es immer eine Steigung gibt und die Steigung somit niemals 0 sein kann. Die Funktion hat dann keinen Punkt an dem sie nicht steigt.

---

@Gast ia18:

Du hast einen kleinen Dreher drin; richtig muss es heißen:

Eine Funktion ist monoton wachsend, wenn die Steigung >=0 ist, oder schöner: Wenn sie ≥ 0 ist.

---

Sorry, fix mit dem Handy getippt. So ist es natürlich korrekt :-)

---

Kein Problem :-)