Kinetik: Gleichförmige Bewegung
Anton startet um 8:00 Uhr in Innsbruck mit einer konstanten Geschwindigkeit von \( 15 \mathrm{~km} / \mathrm{h} \) mit dem Rad Richtung Telfs, das \( 30 \mathrm{~km} \) entfernt ist. Gleichzeitig geht ihm Beate mit einer Geschwindigkeit von \( 5 \mathrm{~km} / \mathrm{h} \) von Telfs Richtung Innsbruck entgegen.
a) Stelle die Gleichungen \( \mathrm{s}_{\mathrm{A}}(\mathrm{t}) \) und \( \mathrm{s}_{\mathrm{B}} \) (t) der Weg-Zeit-Funktionen von Anton und Beate auf, wobei s die Entfernung in \( \mathrm{km} \) und \( \mathrm{t} \) die Zeit in \( \mathrm{h} \) ab 8:00 Uhr angibt.
\( s_{A}(t)=15 \cdot t \)
\( \mathrm{s}_{\mathrm{B}}(\mathrm{t})=30-5 \cdot \mathrm{t} \)
b) Stelle die beiden Weg-Zeit-Funktionen in einem Diagramm dar.
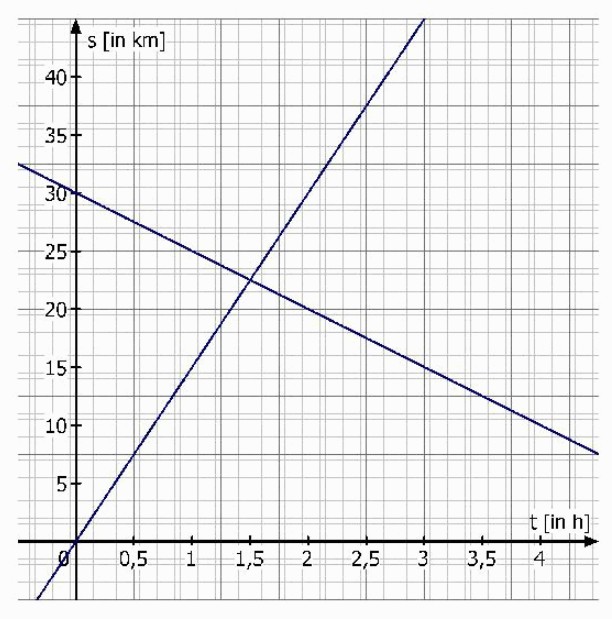
c) Berechne, wann und in welcher Entfernung von Innsbruck sie einander begegnen. Kontrolliere dein Ergebnis mit Hilfe der Skizze.
\( s_{A}(t)=s_{B}(t) \)
\( 15 \cdot t=30-5 \cdot t \)
\( 20 \cdot t=30 \)
\( t=1.5 h \)
\( s_{A}(15)=15 \cdot 1.5=22.5 \mathrm{~km} \)
\( \mathrm{s}_{\mathrm{B}}(\mathrm{t})=30-5 \cdot 1.5=22.5 \mathrm{~km} \)
Sie treffen sich nach \( 1.5 \mathrm{~h} \) in einer Entfernung von \( 22.5 \mathrm{~km} \) von Innsbruck.