Gleichung 2^x − 6 * 2^{-x} + 1=0 und Ungleichung 1/(1-x) ≥ 1/x; D = R\ {0, 1}

Question

hallo habe hier zwei aufgabe die ich nicht lösen kann

 

a) 1/(1-x)  ≥ 1/x      D=R \ {0;1}

 

b) 2^x − 6 * 2^-x + 1=0

 

bitte wenn es geht schrittweise

 

mfg

Comments

 2^x − 6 * 2^-x + 1=0          |*2^x

(2^x)^2 - 6 + 2^x = 0       | Subst. 2^x = u

u^2 - 6 + u =0

u^2 + u - 6 = 0           |pq-Formel oder faktorisieren nach Vieta

(u+3)(u-2) = 0

u1 = -3

u2 = 2

Rücksubst. u = 2^x

-3 = 2^x       unmöglich

2 = 2^x ==> x = 1

L = {1}

Kontrolle:

 

 2^x − 6 * 2^-x + 1=0

2^1 - 6*2^{-1} + 1 = 2 - 3 + 1 = 0 ok.

---

D=R\(0;1) ??

Meinst du D = R \ {0,1} ? Also: Keine Division durch 0. Oder soll das ein Intervall sein?

Schau mal hier, was da überhaupt rauskommen könnte: https://www.wolframalpha.com/input/?i=1%2F%281-x%29++≥+1%2Fx

EDIT: Habe gemäss Kommentar oben D = R \ {0,1} gesetzt.

---

danke erstmal..hab aber eine verständnisfrage. 2x − 6 * 2-x + 1=0 |*2x wieso nimmst du hier *2x?

---

2^{-x} ist ja 1/2^x
Also ein Bruch.

Brüche sind nicht geeignet, wenn man Gleichungen auflösen will.
Daher | * Hauptnenner 2^x

Formeln zu Potenzen z.B. hier: https://www.matheretter.de/wiki/potenzen

---

das ist der definitionsbereich. Alle reellen zahlen außer 0 und 1

Answer 1

zu a)

$$\frac { 1 }{ 1-x } \ge \frac { 1 }{ x }$$

Kritische Stellen:

x = 0 und x = 1

denn an diesen beiden Stellen ist jeweils einer der Brüche nicht definiert, weil sein Nenner Null wird..

Also muss man drei Fälle unterscheiden, nämlich:

x < 0 ,

0 < x < 1

1 < x

 

Fall 1: x < 0

dann ist 1 - x > 0 und x < 0 und es gilt (Multiplikation mit 1 - x  und mit x , dabei muss wegen 1 - x < 0 das Ungleichheitszeichen umgekehrt werden):

$$\frac { 1 }{ 1-x } \ge \frac { 1 }{ x }$$$$\Leftrightarrow x\le 1-x$$$$\Leftrightarrow 2x\le 1$$$$\Leftrightarrow x\le \frac { 1 }{ 2 }$$$${ L }_{ 1 }=\left\{ { x\in  }R|{ x<0\wedge x\le \frac { 1 }{ 2 }  } \right\} =\left\{ { x\in  }R|{ x<0 } \right\}$$

 

Fall 2: 0 < x < 1

dann ist

1 - x > 0 und x > 0 und es gilt

$$\frac { 1 }{ 1-x } \ge \frac { 1 }{ x }$$$$\Leftrightarrow x\ge 1-x$$$$\Leftrightarrow 2x\ge 1$$$$\Leftrightarrow x\ge \frac { 1 }{ 2 }$$$${ L }_{ 2 }=\left\{ { x\in  }R|0<x<1{ \wedge x\ge \frac { 1 }{ 2 }  } \right\} =\left\{ { x\in  }R|{ \frac { 1 }{ 2 } \le x<1 } \right\}$$

 

Fall 3: 1 < x

dann ist

1 - x < 0 und x > 0 und es gilt (gleiche Rechnung wie bei Fall 1, aber wegen anderer Fallvoraussetzung ergibt sich für die Lösungsmenge:

$${ L }_{ 3 }=\left\{ { x\in  }R|{ 1<x\wedge x\le \frac { 1 }{ 2 }  } \right\} =\left\{ \quad  \right\}$$

 

Die Lösungsmenge der Ungleichung ist nun die Vereinigungsmenge der Lösungsmengen der drei Fälle, also:

$$L={ L }_{ 1 }\cup { L }_{ 2 }\cup { L }_{ 3 }$$$$=\left\{ { x\in  }R|{ x<0 } \right\} \cup \left\{ { x\in  }R|{ \frac { 1 }{ 2 } \le x<1 } \right\} \cup \left\{ \quad  \right\}$$$$=\left\{ { x\in  }R|{ x<0 }\vee { \frac { 1 }{ 2 } \le x<1 } \right\}$$

 

zu b)

$${ 2 }^{ x }-6*{ 2 }^{ -x }+1=0$$Beide Seiten mit 2 ^x multiplizieren:$$\Leftrightarrow { { \left( { 2 }^{ x } \right)  }^{ 2 } }+{ 2 }^{ x }-6=0$$$$\Leftrightarrow { { \left( { 2 }^{ x } \right)  }^{ 2 } }+{ 2 }^{ x }=6$$Nun die quadratische Ergänzung bestimmen. Dazu 2 ^x  durch die Wurzel aus dem quadratischen Glied, also durch 2 ^x und durch 2 dividieren und das Ergebnis quadrieren. Es ergibt sich die quadratische Ergänzung 1 / 4 . Diese auf beiden Seiten addieren:$$\Leftrightarrow { { \left( { 2 }^{ x } \right)  }^{ 2 } }+{ 2 }^{ x }+\frac { 1 }{ 4 } =6+\frac { 1 }{ 4 } =\frac { 25 }{ 4 }$$Die linke Seite mit Hilfe der zweiten binomischen Formel als Quadrat schreiben:$$\Leftrightarrow { \left( { 2 }^{ x }+\frac { 1 }{ 2 }  \right)  }^{ 2 }=\frac { 25 }{ 4 }$$"Wurzel ziehen":$$\Leftrightarrow { { 2 }^{ x }+\frac { 1 }{ 2 }  }=\pm \frac { 5 }{ 2 }$$$$\Leftrightarrow { 2 }^{ x }=-3\vee { 2 }^{ x }=2$$2 ^x = - 3 hat keine reelle Lösung, also verbleibt:$$\Leftrightarrow { 2 }^{ x }=2$$$$\Leftrightarrow { 2 }^{ x }={ 2 }^{ 1 }$$$$\Leftrightarrow x=1$$

Answer 2

 

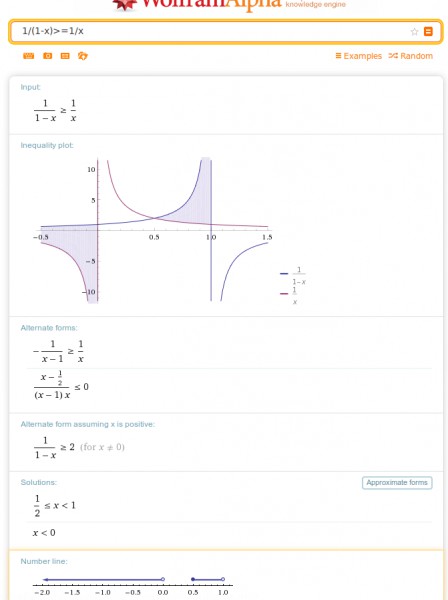
a) 1/(1-x)  ≥ 1/x      D=R\(0;1)

Hier können wir eine Fallunterscheidung durchführen: 1. x > 1, 2. x <0

1. x > 1

1/(1-x) ≥ 1/x | * x

x/(1-x) ≥ 1 | * (1-x), da x > 1, ist (1-x) < 0, deshalb dreht sich das Ungleichheitszeichen um:

x ≤ 1 - x | + x

2x ≤ 1

x ≤ 0,5

Dies steht im Widerspruch zur Voraussetzung

2. x < 0

1/(1-x) ≥ 1/x | * x, da x < 0 dreht sich das Ungleichheitszeichen um:

x/(1-x) ≤ 1 | * (1-x), da x < 0, ist (1-x) positiv, so dass sich das Ungleichheitszeichen nicht verändert

x ≤ 1 - x | + x

2x ≤ 1

x ≤ 1/2

Voraussetzung war, dass x < 0, also gilt die Ungleichung für x < 0

 

Für Aufgabe b) hast Du ja schon das Stichwort gegeben: Substitution

Wir setzen 2^x = u und erhalten aus

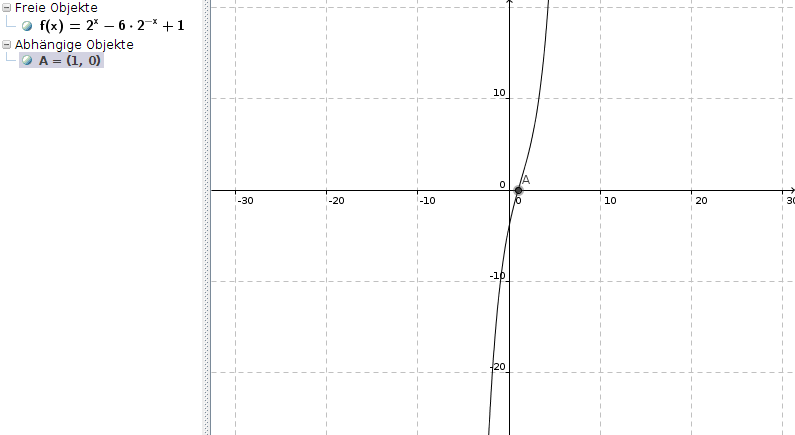
b) 2^x − 6 * 2^-x + 1=0

u - 6 * 1/u + 1 = 0 | da 2^-x = 1/2^x = 1/u

Beide Seiten mit u multiplizieren

u² - 6 + u = 0

u² + u - 6 = 0

pq-Formel

u_1,2 = -1/2 ± √(1/4 + 24/4) = -1/2 ± √(25/4) = -1/2 ± 5/2

u₁ = 4/2 = 2

u₂ = -6/2 = -3

 

2^x = 2

x = 1

 

2^x = -3 | Logarithmus zur Basis 2

x = log₂(-3)

x = ln(-3)/ln(2)

Keine Lösung, da ln(-3) keine Lösung hat.

 

Probe:

2¹ - 6 * 2^-1 + 1 = 2 - 6 * 1/2¹ + 1 = 2 - 3 + 1 = 0 | stimmt :-)

 

Besten Gruß