Zum Trigonometrievideo der Zaps 2014, Hypotenuse als Gegenkathete?

Question

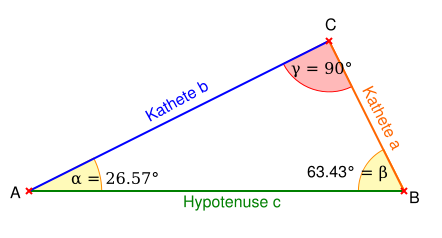
Wenn man bei Trigonometrie:

sin(∝)= Gegenkathete : Hypotenuse       rechnet, ist ja klar, was die Gegenkathete (a), die Ankathete (b) und die Hypotenuse ist (c),

wenn man aber: von γ ausgeht, dann ist ja nicht klar, was An-/Gegenkathete und was die Hypotenuse ist.

Es ist zwar klar, dass dieser Winkel 90° beträgt, aber wenn man die Formel zum Beispiel umstellen möchte, um eine andere Variable auszurechnen, könnte man das brauchen, da der Winkel ja schon gegeben ist.

Also wie bestimmt man das hier jetzt genau?

Answer 1

In einem rechtwinkligen Drieeck ist die Gegenkathete eines Winkels immer die ihm gegenüberliegende Seite.
Die Gegen"kathete" des rechten Winkels gamma ist daher die Hypotenuse.
Du könntest also rechnen:

sin ( gamma ) = Gegen"kathete" / Hypotenuse = Hypotenuse / Hypotenuse = 1

<=> gamma = arcsin ( 1 ) = 90 °

Welch Wunder :-)

Es ist sinnlos, beim Rechnen in rechtwinkligen Dreiecken, in denen gamma der rechte Winkel ist, den Ausdruck sin ( gamma ) in irgendeiner Formel zu verwenden und auflösen / umstellen zu wollen, denn da der rechte Winkel gamma immer 90 ° groß ist, ist sin ( gamma ) immer gleich 1.
Wenn also gamma der rechte Winkel ist, dann hat sin ( gamma ) immer den Wert 1.

Man kann also statt des Ausdrucks sin ( gamma ) immer 1 schreiben..