bzgl. Amplitude siehe hier
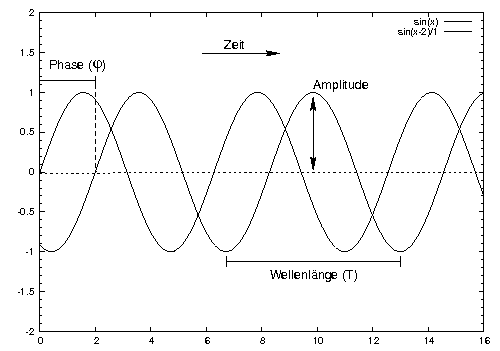
Quelle: http://193.197.131.9:4242/akustische_grundlagen/
Normalerweise hat man folgende schreibweise \( A\cdot sin(\omega t + \phi) \) mit
A = Amplitude
\(\omega\) = Kreisfrequenz
\(\phi\) = Phase
Die Gleichung löst man wie folgt
Es gilt \( sin\frac{x}{2}=\sqrt{ \frac{1-cos(x)}{2} } \)
Setzte z=cos(x) dann muss man folgende Gleichung lösen $$ 2\sqrt{ \frac{1-z}{2}}=3z $$ und die Lösung ist \( \frac{1}{9}\pm \frac{\sqrt{19}}{9} \).
Von diesem Wert den arccos bilden ergibt die Lösung.