Die Eisenbahnlinie zwischen den Städten Solingen und Remscheid im Bergischen Land führt über eine Stahlbrücke. Das Bild unten zeigt, dass der parabelfömige Brückenbogen mit einer Behelfsbrücke zusammengesetzt wurde. Zur Kontrolle wurden während der Montage die Abstände zur Behelfsbrüccke laufend gemessen und mit zuvor berechneten Werten im Bauplan verglichen.
Durch die Wahl des Koordinatensystems liegt der Scheitelpunkt der Parabel genau auf der y-Achse. Somit gilt der Ansatz fur die Funktionsgleichung \( y=\operatorname{ax}^{2}+\mathrm{c} \).
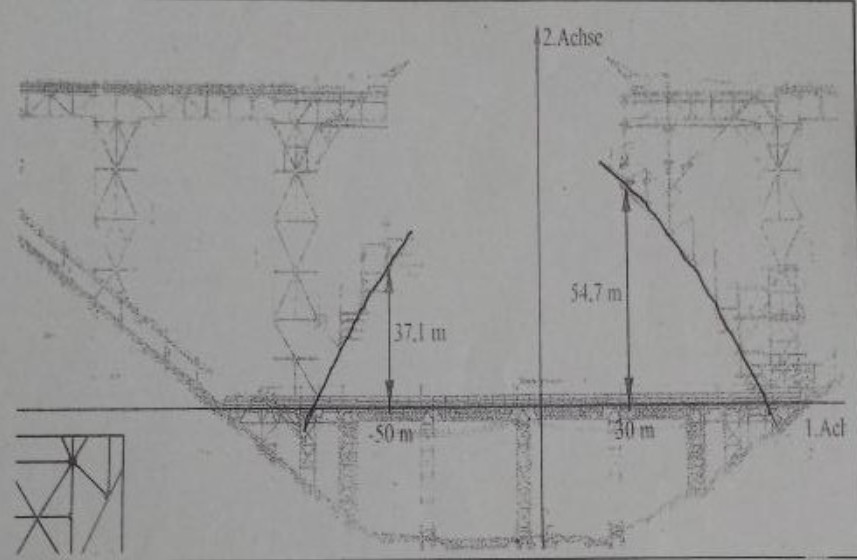
a) Bestimmen Sie für den unteren Parabelbogen der Brücke die Parameter a und c mithilfe der in der Zeichnung angegeben Maße. Geben Sie die quadratische Gleichung mit den errechneten Parametern an.
Im Weiteren wird die Funktionsgleichung mit \( y=-0.011 x^{2}+64,6 \) beschrieben.
b) Berechnen Sie die Höhe unter dem Parabelbogen bei \( -20 \mathrm{~m} \) und \( 0 \mathrm{~m} \). Bei \( -80 \mathrm{~m} \) und bei \( 80 \mathrm{~m} \) ruht der Bogen auf großen Auflagekörpern. Bei wie viel Meter (m) unterhalb der Behelfsbrücke ist das der Fall?
c) Berechnen Sie, in welcher Entfernung von der \( y \)-Achse der Parabelbogen die Behelfsbrücke trifft.