Also.
a) Das müsstest du ja eigentlich können, ist eigentlich schon vorher vorausgesetzt. Für die Schnittpunkte mit der x-Achse setzt du die Funktion gleich 0:
0 = x4 - 8x3 + 16x2 |:x² →Teilen durch x erzeugt immer x = 0 als mögliche Lösung
0 = x² - 8x + 16 |wird durch die 2. binomische Formel zu...
0 = (x - 4)² |√
0 = x - 4 |+ 4
x = 4
Also gibt es zwei Schnittpunkte mit der x-Achse, bei (0|0) und (4|0).
Der Schnittpunkt mit der y-Achse, von denen es ja immer nur einen gibt, ist also auch bei (0|0).
b) Der Nachweis von Extrempunkten (also Hoch- oder Tiefpunkten) ist immer: f'(x) = 0, f''(x) ≠ 0. Bei Hochpunkten muss zusätzlich gelten f''(x) < 0, bei Tiefpunkten f''(x) > 0.
Also stellst du erst einmal die Ableitungen auf:
f'(x) = 4x³ - 24x² + 32x
f''(x) = 12x² - 48x + 32
Angegeben sind die x-Koordinaten 0, 2 und 4. Die setzt du jetzt nacheinander in die Ableitungen ein, um die Punkte nachzuweisen. 2 musst du auch noch in die Ursprungsfunktion einsetzen, um die y-Koordinate nachzuweisen.
f'(0) = 4·0³ - 24·0² + 32·0 = 0 →Extrempunkt bei 0 bewiesen
f''(0) = 12·0² - 48·0 + 32 = 32 →Tiefpunkt bei 0 bewiesen
f(2) = 2⁴ - 8·2³ + 16·2² = 16 - 64 + 64 = 16→Punkt (2|16) bewiesen
f'(2) = 4·2³ - 24·2² + 32·2 = 32 - 96 + 64 = 0 →Extrempunkt bei 2 bewiesen
f''(2) = 12·2² - 48·2 + 32 = 48 - 96 + 32 = -32 →Hochpunkt bei 2 bewiesen
f'(4) = 4·4³ - 24·4² + 32·4 = 256 - 384 + 128 = 0 →Extrempunkt bei 4 bewiesen
f''(4) = 12·4² - 48·4 + 32 = 192 - 192 + 32 = 32 →Tiefpunkt bei 4 bewiesen
c) So sieht die Ableitungsfunktion aus:
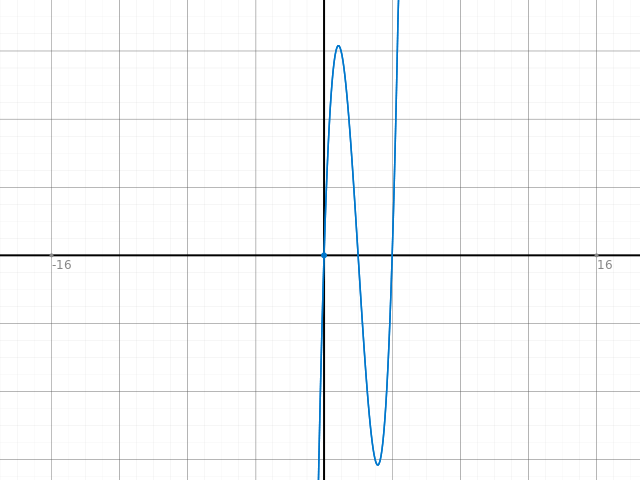
Am Graphen siehst du zwei Extremstellen. Hat die Ableitung einer Funktion einen Extrempunkt, hat die Funktion an dieser Stelle eine Wendestelle, das ist die Stelle, in der die Rechtskrümmung der Funktion in eine Linkskrümmung bzw. andersrum übergeht.
Die Funktion hat also zwei Wendepunkte, diese liegen schätzungsweise bei x=3/4 und x=3.
d1) ist leicht. Du hast ja schon oben aus der Funktion x² ausgeklammert. Die Funktion f ist x2·(x2-8x+16). So siehst du offensichtlich, dass a 16 sein muss.
d2) ist etwas schwieriger, du bestimmst die allgemeine zweite Ableitung von ga(x) = x⁴ - 8x³ + ax²:
ga'(x) = 4x³ - 24x² + 2ax
ga''(x) = 12x² - 48x + 2a
An Wendestellen ist die zweite Ableitung gleich 0, also
0 = 12·0² - 48·0 + 2a = 2a |:2
a = 0
Bei a = 0 liegt bei x = 0 eine Wendestelle vor.
Ich wünsche dir viel Glück bei deiner Arbeit!
LG Florian