Intervall, Prozentanteil, Mittelwert, Standardabweichung..

Question

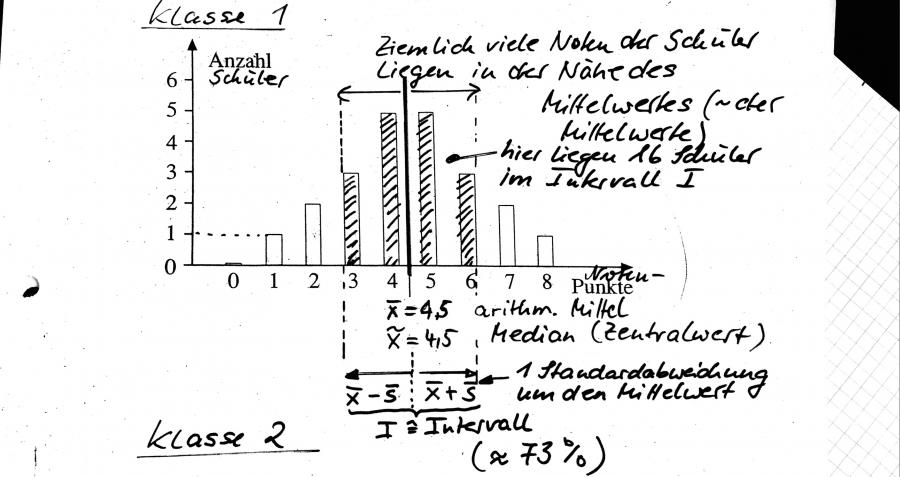
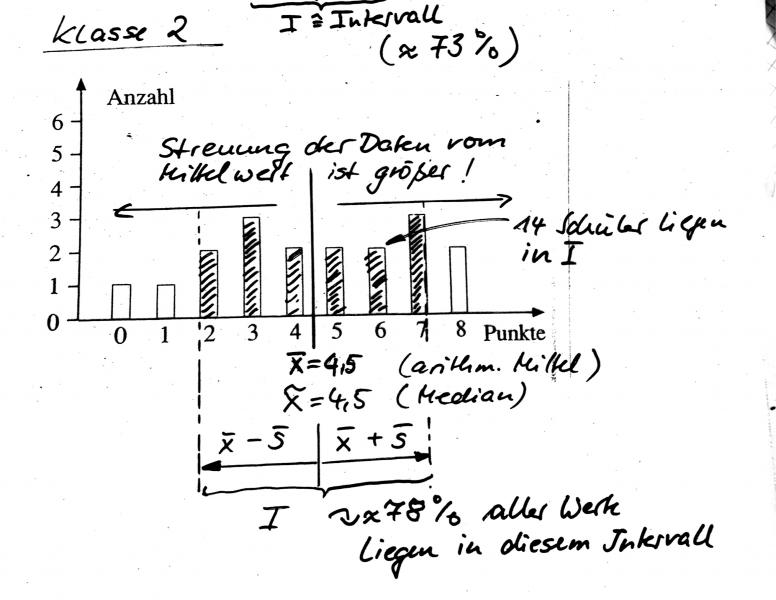
Berechnen SIe angenähert, welcher Prozentanteil der Daten in demjenigen Intervall liegt, welches vom Mittelwert jeweils eine Standardabweichung weit nach links und nach rechts reicht, also \( \overline{\mathrm{x}}-\overline{\mathrm{s}} \) bis \( \overline{\mathrm{x}}+\overline{\mathrm{s}} \)

Gruppe 1:  4,8,4,6,7,5,4,6,5,7,5,2,1,4,6,5,4,3,5,2,3,3

Gruppe 2:  5,6,5,3,7,2,6,2,6,3,1,8,7,2,0,4,7,4,8,3

Ich habe diese Frage schon einmal zuvor gestellt, aber ich glaube mein Problem zu undeutlich dargestellt. Deshalb habe ich hier etwas umgestellt.

Ich verstehe die Aufgabe nicht. Dazu habe ich Lösungen welche ich unten Beifügen werde. Könnt ihr mir erklären wie ich zu den Lösungen komme? :)

Comments

Es wäre glaube ich besser gewesen wenn du erklärst was du nicht verstehst.
1. Kannst du den Mittelwert x ausrechnen?

2. Kannst du die Standardabweichung s bilden?

3. Kannst du vom Intervall [x - s, x + s] die Intervallgrenzen bestimmen?

4, Kannst du bestimmen wie viel Prozent aller Werte in diesem Intervall liegen?

Geht diese Schritte anhand deiner Lösung durch und schau wo du dazu etwas findest und schau ob du es verstehst. Und wenn du es nicht verstehst dann sag genau was du nicht verstehst.

---

Bitte entschuldige mich,den einzigen Schritt, den ich verstehe ist-ich kann den Mittelwert bestimmen. Aber ich bräuchte hilfe bei der Standardabweichung, beim Intervall und beim Prozent berechnen aller werte, die im Intervall liegen :)

Answer 1

Ich mache dir das mit dem Mittelwert und der Standardabweichung von Gruppe 1 vor und du machst es dann mit Gruppe 2 nach

Gruppe 1:  4,8,4,6,7,5,4,6,5,7,5,2,1,4,6,5,4,3,5,2,3,3

Ich sortiere die Werte etwas:

1 22 333 44444 55555 666 77 8 
1·1, 2·2, 3·3, 5·4, 5·5, 3·6, 2·7, 1·8

Mittelwert μ = (1·1 + 2·2 + 3·3 + 5·4 + 5·5 + 3·6 + 2·7 + 1·8)/22 = 4.5

Standardabweichung: σ^2 = (1·(1 - 4.5)^2 + 2·(2 - 4.5)^2 + 3·(3 - 4.5)^2 + 5·(4 - 4.5)^2 + 5·(5 - 4.5)^2 + 3·(6 - 4.5)^2 + 2·(7 - 4.5)^2 + 1·(8 - 4.5)^2)/22 = 131/44
σ = √(131/44) = 1.73

Das Intervall ergibt sich aus 

[μ - σ, μ + σ] ≈ [2.77, 6.23] ≈ [3, 6]

Im Intervall von 3 bis 6 liegen 16 Werte. Das sind 16/22 = 72.73% ≈ 73%

 

Bitte mache das jetzt genau so für Gruppe 2 nach.