Aufgabe:
Im Maßstab 1:5000 sieht man eine Passtraße von oben. Sie beginnt an Punkt A und erreicht B die Passhöhe. Punkt A befindet sich auf einer Höhe von 620m, die durchschnittlich Steigung beträgt 14%. Wie hoch liegt Punkt B und wie weit fährt man von A bis B.
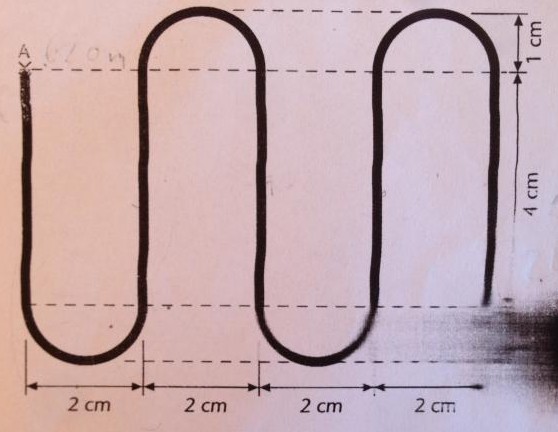
Ich hab schon einen Lösungsansatz für die Strecke, ich glaube aber das der falsch ist:
Sleigungswinkel \( \tan ^{-1}(0,14)=7,96 \)
\( \tan (\alpha)=620 \mid : \tan (7,96) \)
\( x=\frac{620}{\operatorname{lan}(7,96)} \)
\( x=4433,98 \mathrm{~m} \) Strecke