Nutze die Defiitionen des Erwartungswertes und der Varianz, um aus den Angaben der Aufgabenstellung die Einzelwahrscheinlichkeiten für die Werte von X zu berechnen.
$$E[X]=0$$$$\Leftrightarrow (-1)*P(X=-1)+0*P(X=0)+1*P(X=1)=0$$$$\Leftrightarrow (-1)*P(X=-1)+1*P(X=1)=0$$$$\Leftrightarrow P(X=1)=P(X=-1)$$
$$Var[X]=0,4$$$$\Leftrightarrow$$$$(-1-E[X])^{ 2 }*P(X=-1)+(0-E[X])^{ 2 }*P(X=0)\\+(1-E[X])^{ 2 }*P(X=1)=0,4$$$$\Leftrightarrow$$$$ (-1-0)^{ 2 }*P(X=-1)+(0-0)^{ 2 }*P(X=0)+(1-0)^{ 2 }*P(X=1)=0,4$$$$\Leftrightarrow P(X=-1)+P(X=1)=0,4$$Wegen P ( X = - 1 ) = P ( X = 1 ) (siehe oben):$$\Leftrightarrow P(X=1)+P(X=1)=0,4$$$$\Leftrightarrow P(X=1)=0,2$$
Also:
$$P(X=-1)=P(X=1)=0,2$$$$P(X=0)=1-2*0,2=0,6$$
Somit sieht die Skizze der Wahrscheinlichkeitsfunktion so aus:
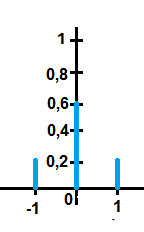
und die Skizze der Verteiungsfunktion so: