Berechne die Helligkeit / pro Meter Wassertiefe

Question

Unter Wasser nimmt die Helligkeit exponentiell ab, pro Meter Wassertiefe um 11 %

a) Stellen sie die Funktionsgleichung auf.

b)  zeichnen sie den graphen für diesen Vorgang  bis zu einer wassertiefe von 30 Metern.

c) Berchnen sie in welcher wassertiefe die helligkeit auf 50% des Ausgangswertes (100 %) gesunken ist.


Wer mag der Peggi helfen...?

herzlichen Gruß

Answer 1

Hallo nochmal Peggi :-)

 

a) Funktionsgleichung

Auf Meeresspiegel herrscht die Helligkeit x, 

in einem Meter Tiefe 11% weniger, also x - 11%, also 0,89 * x,

in zwei Metern Tiefe beträgt die Helligkeit entsprechend (x - 11%) - 11% = (0,89 * x) * 0,89 = 0,89² * x

usw.

Man kann also allgemein sagen, dass die Helligkeit h in Abhängigkeit von der Meterzahl x so als Funktionsgleichung dargestellt werden kann:

h(x) = 0,89^x

 

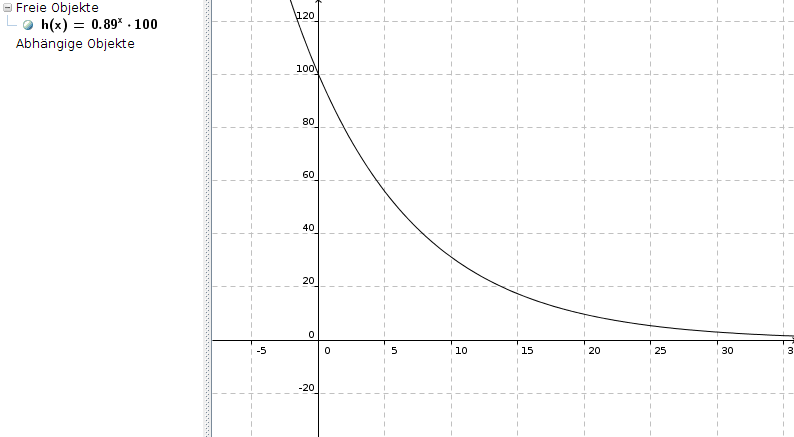
b) Graph bis 30 Metern Tiefe

Hier habe ich statt h(x) = 0,89^x geschrieben h(x) = 0,89^x * 100, um die Helligkeit in Prozenten auszudrücken:

 

c) In welcher Wassertiefe ist die Helligkeit auf 50% gesunken?

Wir bleiben bei h(x) = 0,89^x

Bei einem Meter Wassertiefe liegen wir wie oben gesagt bei 89%,

bei zwei Metern bei 0,89 * 0,89 = 0,7921 = 79,21% usw.

Wann liegen wir also bei 50%?

h(x) = 0,89^x = 50% = 0,5

0,89^x = 0,5

Nun kommt das, was Dir bei der Antwort von Unknown vielleicht unklar war:

Um das x zu isolieren, müssen wir auf beiden Seiten der Gleichung den Logarithmus zur Basis 0,89 ziehen:

x = log_0,89(0,5)

Und hier darf man einfach rechnen ln(Logarithmand 0,5) / ln(Basis 0,89), also

ln(0,5)/ln(0,89) ≈ 5,9480346807

 

Das heißt, wie schon als Antwort gegeben:

Bei einer Wassertiefe von ca. 5,95 Metern haben wir eine Helligkeit von nur noch 50%.

 

Etwas klarer?

 

Liebe Grüße

Andreas

Comments

Noch eine kurze Ergänzung zum letzten Schritt:

 

0,89^x = 0,5

Was ich geschrieben habe, ist die Kurzfassung, ausführlich sieht es so aus:

ln(0,89^x) = ln(0,5)

und da ln(a^b) = b * ln(a), folgt

x * ln(0,89) = ln(0,5) | : ln(0,89)

x = ln(0,5)/ln(0,89)

---

"in zwei Metern Tiefe beträgt die Helligkeit entsprechend (x - 11%) - 11% = (0,89 * x) * 0,89 = 0,892 * x"

------------

Aha: (x - 11%) - 11% = (0,89 * x) * 0,89

-----------

Sorry, das ist mathematischer Unsinn ...

---

@Gast:

Mathematisch wohl nicht ganz sauber, aber zur Verdeutlichung sicherlich ganz gut geeignet, oder nicht?

Answer 2

Hi Peggi,

ich versuche mich mal ;).


a) es bleibt also 89% übrig. Das sind 0,89

y = 0,89^x

Dabei ist x die Anzahl in Meter und y die prozentualle Helligkeit. (*100 in Prozent)


b) Das überlasse ich Dir ;).


c)

y = 0,89^x = 0,5   |ln

xln(0,89) = ln(0,5)

x = ln(0,5)/ln(0,89) ≈ 5,95


Nach etwa 5,95 m haben wir nun noch 50% des Lichts.

Einverstanden?


Grüße

Comments

verstehe den Rechenschnitt nicht..