Bestimmen Sie alle Schnittpunkte der Tangente und Wendetangenten von Γ_f

Question

Aufgabe:

Bestimmen Sie alle Schnittpunkte der Tangenten in \( x_0 = -1 \) an den Graphen \( \Gamma _ { f } \) der Funktion \( f ( x ) = x ^ { 4 } - 3 x ^ { 2 } - 4 x + 3 \) mit \( \Gamma _ { f } \) und Wendetangenten von \( \Gamma _ { f } \). Skizzieren Sie anschließend den Graph \( \Gamma _ { f } \) der Funktion und Wendetangenten von \( \Gamma _ { f } \).

Was hat diese Aufgabe mit dem Taylorpolynom zu tun? Wie bestimme ich hier den Wendepunkt bzw, die Wendetangente?

Ich bin etwas verwirrt wegen des Taylorpolynoms.

Answer 1

f(x) = x^4 - 3x^2 - 4x + 3
f '(x) = 4x^3 - 6x - 4
f ''(x) = 12x^2 - 6

 

Tangente an der Stelle -1

f(-1) = 5
f '(-1) = -2

t(x) = -2 * (x + 1) + 5 = -2x + 3

 

Wendetangenten

f ''(x) = 0
12x^2 - 6 = 0
x = +- √0.5

f(√0.5) = 7/4 - 2√2
f '(√0.5) = - 2√2 - 4

 

f(-√0.5) = 2√2 + 7/4
f '(-√0.5) = 2√2 - 4

tw1(x) = (-2√2 - 4) * (x - √0.5) + 7/4 - 2√2 = 15/4 - x·(2√2 + 4)

tw2(x) = (2√2 - 4) * (x + √0.5) + 2√2 + 7/4 = x·(2√2 - 4) + 15/4

 

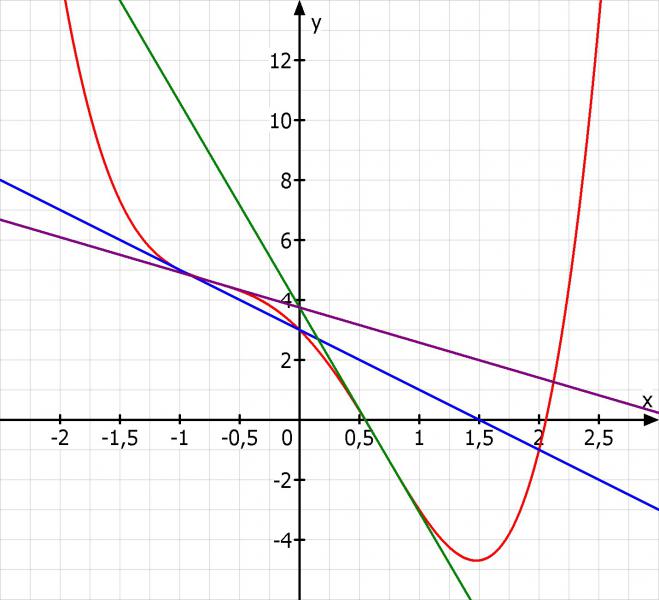
Skizze:

Comments

Schnittpunkte:

t(x) = tw1(x)
-2x + 3 = 15/4 - x·(2√2 + 4)
x = 3√2/8 - 3/8
t(3√2/8 - 3/8) = 15/4 - 3√2/4

S1(3√2/8 - 3/8 | 15/4 - 3√2/4)
S1(0.1553, 2.6893)

 

t(x) = tw2(x)
-2x + 3 = x·(2√2 - 4) + 15/4
x = -3√2/8 - 3/8
t(-3√2/8 - 3/8) = 3√2/4 + 15/4

S2(-3√2/8 - 3/8, 3√2/4 + 15/4)
S2(-0.9053, 4.8107)

---

danke dir Der_Mathecoach :D
jetzt fühl ich mich bei meiner Rechnung viel sicherer.