Beweise für einen selbstkomplementären Graphen

Question

Das Komplement \( \bar{G} \) eines Graphen \( G \) mit \( v(G)=n \) ist definiert durch \( \bar{G}:=G_{n}-E(G) \), dabei ist \( G_{n} \) der vollstandige Graph mit \( n \) Knoten

a) Zeichnen Sie das Komplement des folgenden Graphen.

Ein Graph heiBt selbstkomplementär, falls er isomorph zu seinem Komplement ist (der Graph aus a) ist ein Beispiel fïr einen selbstkomplementären Graphen).

b) Beweisen Sie, dass für einen selbstkomplementären Graphen \( G \) gilt:

\( (v(G) \equiv 0 \bmod 4) \) oder \( (v(G) \equiv 1 \bmod 4) \)

Hinweis: Ein vollständiger Graph mit \( n \) Knoten hat laut Vorlesung \( \frac{\mathrm{n}(n-1)}{2} \) Kanten, für welche \( n \) ist diese Zahl durch 2 teilbar? Was hat dies mit der Aufgabenstellung zu tun?

c) Geben Sie bis auf Isomorphie alle selbstkomplementären Graphen mit 4 Knoten an.

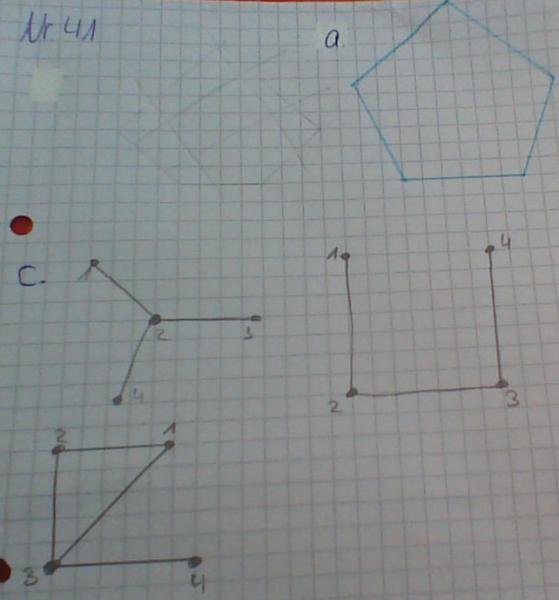
Ich hoffe dass ich Aufgabe a und c verstanden habe, kann sich das jemand anschauen?

Aufgabe b verstehe ich nicht wie ich das beweisen soll einfach mit Module?

Answer 1

zu a)

Ein komplementärer Graph besitzt die gleichen Knoten wie der Ursprungsgraph, unterscheidet sich aber in seinen Kanten, d. h. der Komplementgraph besitzt genau die Kanten, die der Ursprungsgraph nicht hat.

Deine Knoten sind gleich und die Kanten sind unterschiedlich -> stimmt also.

zu b) ein Versuch ..

Ein Graph G heißt selbstkomplementär, wenn der komplementäre Graph G* zu G isomorph ist. Bei Vorliegen von Isomorphie haben beide Graphen gleich viele Knoten und Kanten.

G* und G sind insgesamt "vollständig", denn dort wo in G eine Kante ist, ist in G* keine Kante vorhanden und umgekehrt. G* und G haben zusammen die doppelte Anzahl der Kanten vom Graphen, da der komplementäre Graph und Graph die gleiche Anzahl von Kanten haben.

Für diese "Vollständigkeit" als Graph gilt in Bezug auf die Kantenzahl: (1/2)*n/(n - 1)

G* und G haben gleich viele Kanten, also insgesamt (1/2)*n/(n - 1). Folglich hat G dann (1/2)*(1/2)*n/(n - 1) = (1/4)*n/(n - 1) Kanten.