Nullstellen von sin(x^2)

Question

Ich soll von einer Funktion extremstellen berechnen. Die erste Ableitung habe ich bestimmt und so weit wie möglich gekürzt. Ich stehe nur noch vor: sin(x^2)=√(2):2 Ich weiß auch dass die Lösung +- 1:2 √(3+8n) * √(pi) ist. Aber wie genau kommt man darauf? Kann man x=sqrt(arcsin(2^0.5:2)) umformen dass man auf die Lösung kommt? Im Unterricht hatte ich eine ähnliche Aufgabe noch nie.

Comments

Damit ich dir weiterhelfen kann bräuchte  ich
die Ausgangsfunktion. mfg Georg

---

Hallo Georg,

danke für das anbieten deiner Hilfe.

Die ursprüngliche Funktion war:

f(x) = 1- √(2)/2 x^2 - cos(x^2)

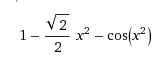
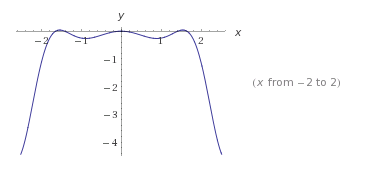
daraus ergibt sich

f'(x) = x * ( 2 sin(x^2) - √(2))  = 0  [Extremstellen finden]

2 sin (x^2) - √(2) = 0 [Satz vom Nullprodukt x0 = 0]

sin(x^2) = √(2)/2

 

Laut Aufgabe soll ich alle Extremstellen zwischen -√(pi) und +√(pi) finden. Eine liegt bei x = 0.

Answer 1

SIN(x^2) = √2/2

x^2 = ARCSIN(√2/2) = pi/4 [Achtung: hier gibt hier mehr als eine Lösung]

x = ± √pi/2

Answer 2

$$\sin x^2=\frac12\sqrt 2$$$$x_1^2=\frac{\pi}4;\quad x_3^2=\frac{3\pi}4$$$$x_{1;2}=\pm\frac12\sqrt{\pi};\quad x_{3;4}=\pm\frac12\sqrt{3\pi}.$$

Answer 3

Hallo simon.sch,

f ( x ) = 1 - √(2)/2 * x²  -  cos ( x² )
f ´( x ) = √(2)/2* 2*x  + sin(x²) * 2 * x
f ´( x ) = 2 * x * sin ( x² ) - x * √ 2
Extremstellen
2 * x * sin ( x² ) - x * √ 2 = 0
2 * x * sin ( x² ) = x * √ 2
1.Lösung : x = 0
2 * sin ( x² ) = √ 2
sin ( x^2 ) = √ 2 / 2
acrsin(sin ( x^2 )) = arcsin(√ 2 / 2);
x^2 = 0.7854
x = ± √ 0.7854
x = 0.8862
x = - 0.8862
So jetzt wird es noch etwas schwieriger.
Die sin Funktion hat unendlich viele
Extremstellen : 90 °, 270 °, 450 ° usw.
Dies vererbt sich auch auf deine
Ausgangsfunktion.
Bitte lass dir einmal die Funktion im
Wertebereich z.B. -5..5 zeichnen.
Dann siehst du noch jede Menge
Extremstellen. Insbesondere noch 2
weitere im angegebenen Wertebereich
Wurzel(pi).
Ich muß mir das aber selbst einmal
klarmachen. Ich esse jetzt erst einmal
zu Abend.
mfg Georg
 

 

Comments

x=sqrt(arcsin(2^0.5:2)) umformen dass man auf die Lösung kommt?
Dies ist mir nicht gelungen.
Bei den anderen Antwortgebern stehen kürzere Terme.
Vielleicht fragst du dort einmal an.
mfg Georg