Aufgabe:
Man muss hier ohne Taschenrechner sin(alpha) und cos(alpha) bestimmen
Problem/Ansatz:
Was wäre der Rechenweg bei c) wenn es um große Winkel geht ? 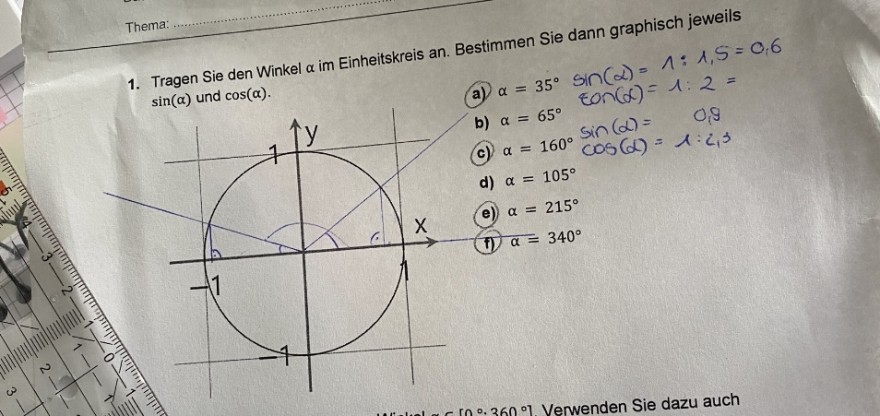
Text erkannt:
Thema:
1. Tragen Sie den Winkel \( \alpha \) im Einheitskreis an. Bestimmen Sie dann graphisch jeweils \( \sin (\alpha) \) und \( \cos (\alpha) \).
a) \( \alpha=35^{\circ} \)
\( \sin (\alpha)=1: 1,5=0.6 \)
b) \( \alpha=65^{\circ} \)
\( \tan (\alpha)=1: 2= \)
c) \( \alpha=160^{\circ} \)
\( \sin (\alpha)=0,9 \)
d) \( \alpha=105^{\circ} \)
(e) \( \alpha=215^{\circ} \)
(i) \( \alpha=340^{\circ} \)