Von Devon aus, unserem letzten Rastplatz, ging es nun weiter. Heute gab es eine gute Vorgabe. Immerhin wurden 135 km geschafft - und das nur an reiner Distanz. Durch Taktieren, um Steigungen zu überwinden, wurden laut Tacho sogar 150 km zurückgelegt!
Aber nichtsdestotrotz blieben ein wenig Zeit und Kraft für einen kleinen Abstecher nach Exeter, um sich dort die Kathedrale anzuschauen:

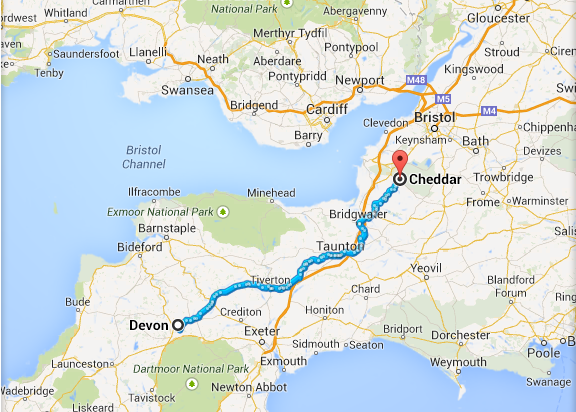
Wir wollen dabei nicht vorenthalten, wie viel Höhenmeter zurückgelegt wurden: 1100 m. Damit kommen wir auch zu unserer Mathe-Challenge. Davor aber noch die obligatorische Landkarte, damit ihr das mit euren Augen verfolgen könnt. Auch wenn das Anschauen nur halb so anstrengend ist, wie es selbst abzuradeln :D
Mathe-Challenge (einfach):
Wie gerade erwähnt wurde eine Distanz von 135 km zurückgelegt. Dabei wurden 1100 m überwunden. Welcher prozentualen Steigung entspricht dies, wenn man von einer gleichmäßigen Steigung ausgeht?
Lösung Mathe-Challenge Tag 2:
Nicht vom Kosinus erschrecken lassen ;-) Den Tipp mit a*cos(bx) + c hattet ihr ja vorgegeben gehabt. Damit könnt ihr direkt die Amplitude a auslesen. Diese muss die Hälfte des Abstandes der y-Werte der Extrema sein. Also der Unterschied ist ja 1 (denn Maximum bei H(0|1) und Minimum bei T(5|0)) und damit a = 0,5. Schauen wir weiter, was wir direkt ablesen können. Das wäre das c. Die Amplitude wird von der Mitte der Extrema aus gemessen. Das wäre in diesem Falle der y-Wert 0,5. Diesen Wert muss nun auch c annehmen.
Setzen wir nun noch Punkt T(5|0) ein, um b zu errechnen:
0 = 0,5*cos(b*5) + 0,5 |-0,5 und dann :0,5
-1 = cos(b*5) |arccos
arccos(-1) = 5b |:5
arccos(-1) / 5 = b
Mit dem Taschenrechner ergibt sich b = 0,628 und das entspricht π/5 = b.
Wir haben also f(x) = 0,5 * cos(π/5 * x) + 0,5
Die maximale Steigung bestimmen wir nun mittels der Ableitungen. Wir wollen die maximale Steigung, also den Wendepunkt.
f‘(x) = 0,5*(π/5) * (-sin(π/5 * x)) = -π/10 * sin(π/5 * x)
f‘‘(x) = -2,5*(π^2/5) * cos(π/5 * x) = -π^2/50 * cos(π/5 * x)
Für den Wendepunkt muss nun f‘‘(x) = 0 sein (sowie f‘‘‘(x) ≠ 0).
f‘‘(x) = -π^2/50 * cos(π/5 * x) = 0
cos(π/5 * x) = 0
In dem für uns interessanten Intervall x ϵ [0;5] reicht es, die allgemeine Lösung des Kosinus für z = π/2 + πk anzuschauen, wenn k = 0 ist.
Also z = π/2 = π/5 * x
x = 2,5
Für x = 2,5 haben wir einen Wendepunkt und damit eine maximale Steigung. Die Steigung dort ist:
f‘(2,5) = - π/10 * sin(π/5 * 2,5) = -π/10 = -0,314
Für unsere Radler ist das also eine Steigung von 31,4 % und er wird wohl getragen werden müssen.