Wieso wird bei dieser Art der Wahrscheinlichkeitsrechnung so gerechnet?

Question

Also folgendes kleines Verständnisproblem:

Angenommen wir haben P=(-0.5<U<0.5)

Dies ist ja dann

0.6915-(1-0.6915)

Was ich nicht verstehe ist, dass Φ(-0.5) =1-Φ(0.5)  aber auch (U>0.5)=1-Φ(0.5)

Hier wäre ja nun der Fall dass

P(U>-0.5) .

Jetzt müsste man doch eigentlich wegen dem - vor der 0.5  1-Φ(0.5) rechnen und da es sich hierbei um >-0.5 handelt auch 1-Φ(0.5) (wegen dem größer gleich statt kleiner gleich welches ja einfach die rechnung Φ(0.5)zur Folge hätte).

Ich verstehe nicht wieso man einfach

0.6915-(1-0.6915) rechnen kann da eigentlich doch 2 mal 1-..... gerechnet werden müsste.

(Ich habe mit der Aufgabe an sich kein Problem nur ich hoffe jemand versteht meine überlegung (verwirrung) und kann mich aufklären)

Vielen Dank und schönes Wochenende

Answer 1

Mal die mal die Glockenkurve auf

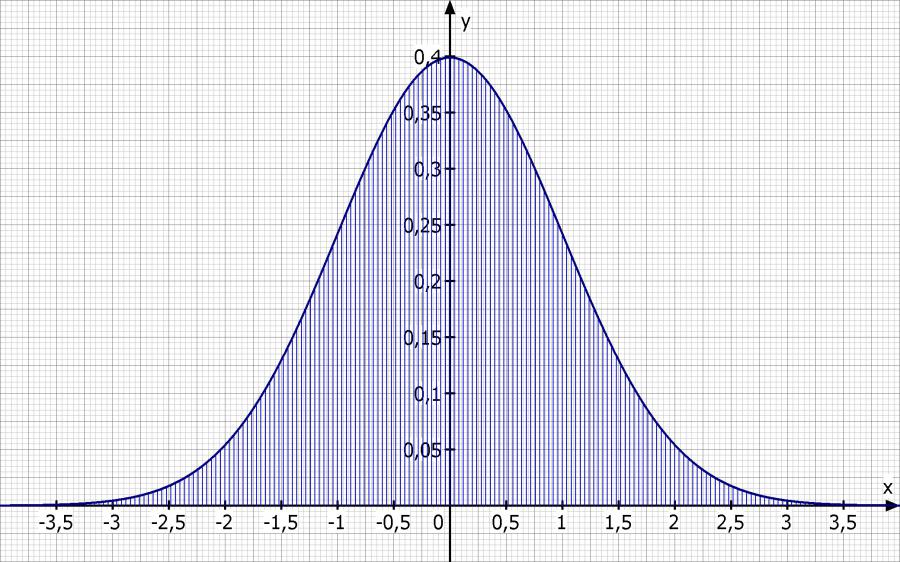
Du möchtest jetzt folgende Wahrscheinlichkeit berechnen

Markiere dir im folgenden die Bereiche die betroffen sind

P(-0.5 < x < 0.5)

= P(x < 0.5) - P(x < -0.5)

= Φ(0.5) - Φ(-0.5)

Nun ist aber Φ(-0.5) genau so groß wie 1 - Φ(0.5). Bitte das optisch nachvollziehen!!

= Φ(0.5) - (1 - Φ(0.5))

= Φ(0.5) - 1 + Φ(0.5)

= 2·Φ(0.5) - 1

mit Φ(0.5) = 0.6915 ergibt sich jetzt

= 2·0.6915 - 1 = 0.383

Comments

Φ(-0.5) =1 - Φ(0.5)

P(x < -0.5) = P(x > 0.5)

Wie gesagt bitte beide bereiche Markieren. Aufgrund der Symmetrie müssen die bereiche gleich sein.