Wie breit ist der Bergsee?

Question

Von einer Aussichtsplattform aus, die auf einem Berggipfel liegt, erscheinen die Ufer eines darunter liegenden Bergsees
unter den Tiefenwinkeln = 65,20 und ß = 47,90 (Fig. 1). Die Plattform ist 1800m vom näher liegenden Seeufer entfernt.
Wie breit ist der See entlang der Sichtlinie?

 

Ich hab 560,64 m raus stimmt das ?

Comments

Korrekt !! 560,37 m ganz genau .

Answer 1

Hi,

ich habe die Skizze nochmals neu gemacht.

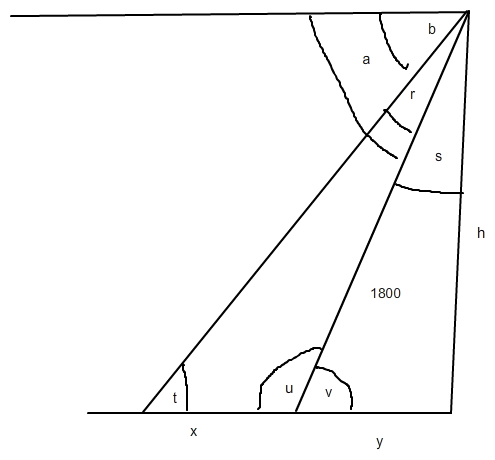
Im rechten Dreieck kann man direkt den unteren Winkel bestimmen: v = 65,2°

(Nofalls über: Der obere Winkel ist ja s = 90°-a...)

Damit hat man im Dreieck, welches von Interesse ist, zwei Winkel (r = a-b = 17,3°) und den Ergänzungswinkel zum gerade errechneten: u = 114,8°

Damit ergibt sich dank Sinussatz a = 1800m*sin(r)/sin(t) = 721,41 m

(Dabei ist t = 180°-114,8°-17,3°)

Ohne Sinussatz/Cosinussatz

Als ersteres berechne h. Du weißt dabei, dass ein rechtwinkliges Dreieck vorliegt und kennst den oberen Winkel sowie die Hypotenuse.

Außerdem kann y berechnet werden.

Mit h und dem oberen Winkel kann dann wieder x+y berechnet werden.

Grüße