Beweise das f(x) genau eine nullstelle besitzt

Question

a) Beweisen Sie, dass
$$ f(x)=\ln (x)+2 x-2 $$
genau eine Nullstelle besitzt.
b) Geben Sie den Definitinionsbereich \( \mathbb{D}_{f} \subset \mathbb{R} \) von \( f \) an.
c) Schlagen Sie ein sinnvolles Vorgehen vor, wie man verfahren sollte, wenn während eines Newtonverfahrens der Definitionsbereich verlassen wird.
d) Führen Sie vom Startpunkt \( x_{0}=0,5 \) drei Iterationen des Newtonverfahrens aus, um die Nullstelle anzunähern.

Leider habe ich keinen Ansatz und brauche einen, da Morgen in der Klausur sowas dran kommen könnte

Comments

Wenn du zeigen kannst, dass deine Funktion stetig ist und du einen Funktionswert grösser als 0 und einen kleiner als 0 hast, die Ableitung zwischen diesen beiden Stellen stikt grösser oder strikt kleiner als 0 ist, dann muss es nach Zwischenwertsatz (welchem?) genau eine Nullstelle geben.

Answer 1

ich versuche mich mal.

a)

Bilde die Ableitung:

f'(x) = 1/x + 2

Zeige, dass für x > 0 das ganze monoton steigend ist. Das ist leicht getan, da f'(x) > 0 für x > 0 ist.

Wenn man nun die Nullstelle nicht direkt sieht (x = 1), so kann man zumindest feststellen, dass für x < 1 f(x) < 0 ist und für x < 1 ist f(x) > 1  -> Eine Nullstelle.

b)

D = R⁺ (Der Numerus muss > 0 sein)

c)

Da bin ich gerade überfragt.

d)

Siehe hier ;).

https://www.mathelounge.de/49035/mathe-artikel-das-newtonverfahren

Grüße

Comments

Danke für die schnelle Antwort, sobald ich alles durchgekaut habe melde ich mich erneut. ;)

---

Tue dies. Vielleicht fällt Dir aus dem Unterricht auch noch was zu c) ein. Würd mich auch interessieren ;). Außer "Nen anderen Startwert wählen." fällt mir da auch nix ein :P. Ist mir noch nie bewusst passiert, oder ich habs nicht bemerkt ^^

---

für c) hab ich leider nichts gefunden.

für d) hat dein Beitrag sehr geholfen. Hier mein Resultat: 

       x1= 0.92

        x2 = 1,02

       x3 = 0.001 

Finde ich realistisch.

---

Da stimmt iwas nicht.

Ich komme auf x ≈ 0,9999...

Probier es nochmals. Du wirst Dich wo vertippt haben ;).

Answer 2

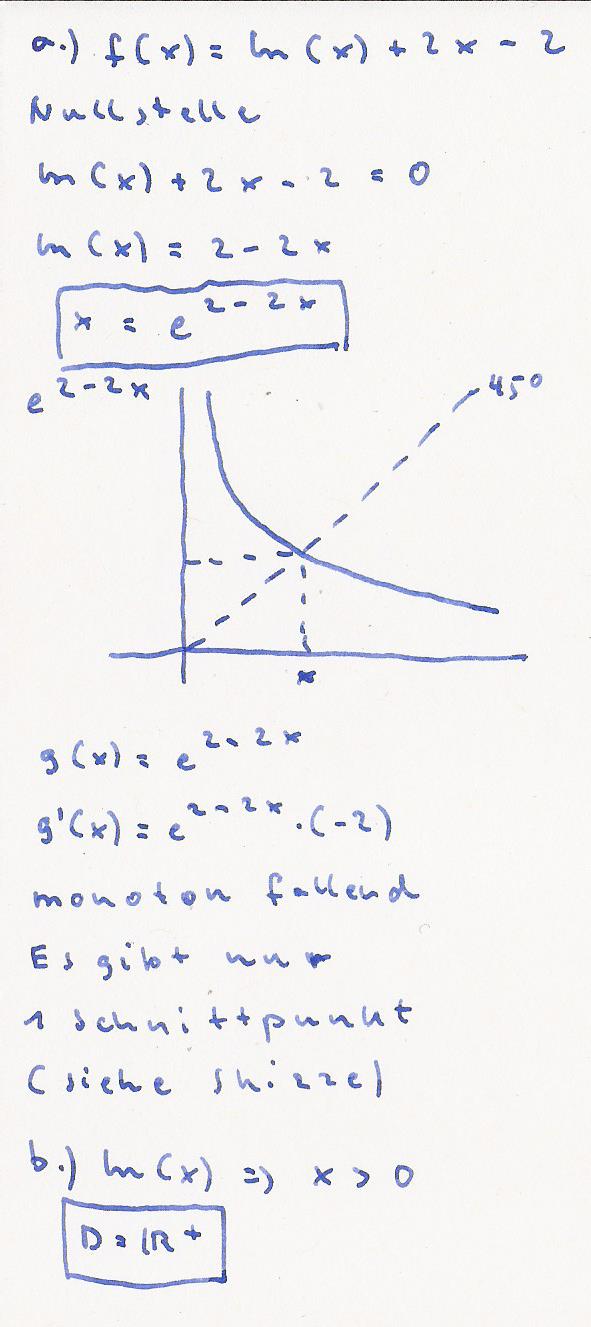
Umgeformt ergibt sich
x = e^{2-2x}
g ( x ) = e^{2-2x}
g ´( x ) = e^{2-2x} *(-2);
Die Funktion ist str.monoton fallend.
( siehe Skizze )
Die Lösung für x = e^{2-2x}
kann nur ein a = a sein und muß
auf der Winkelhalbierenden liegen.
Es gibt nur einen Schnittpunkt zwischen
der Winkelhalbierenden und einer
monoton fallenden Funktion.
Damit wäre bewiesen das es nur 1
Nullstelle gibt.

b ) ln ( x ) kommt vor => x > 0 : D = ℝ⁺

c.) einen höheren Startwert wählen.

d.) Nach den Berechnungen meines
Matheprogramms verläuft die Reihe
beim Newtonverfahren
x = 0.5
x = 0.923
x = 0.998
x = 0.999

Irgendwo muß bei dir ein Fehler sein.
Bin auch noch bereit den Rechengang
hier einszustellen.

mfg Georg