Question

Kann mir jemanden helfen? ich weiß nicht wie ich dies Aufgabe lösen soll....?

Ein Kind von 45 kg Masse sitzt auf einer Hängematte. Diese ist mit Seilen zwischen zwei Mauen aufgehängt; das likne Seil bildet einen Wiinkel von 50° mit der Mauer, rechts haben wir einen Winkel von 75 °. Welche Kraft wirkt in den beiden Seilen?  

Mfg Ivo

Comments

Hatten wir das nicht schon?

---

Dann werde ich nachher eine Lösung einstellen.
Ivo, ich gebe aber zu bedenken das du solche
Aufgaben später selbstständig lösen mußt.

---

Ich habe es schon versucht georgborn und es geht nicht weiter..

Answer 1

Hallo Ivo,
die Lösung dieser Aufgabe ist schwieriger als
die vorhergehenden Aufgaben zum Kräfteparallelogramm,
da bei den anderen Aufgaben Symmetrie vorhanden war.

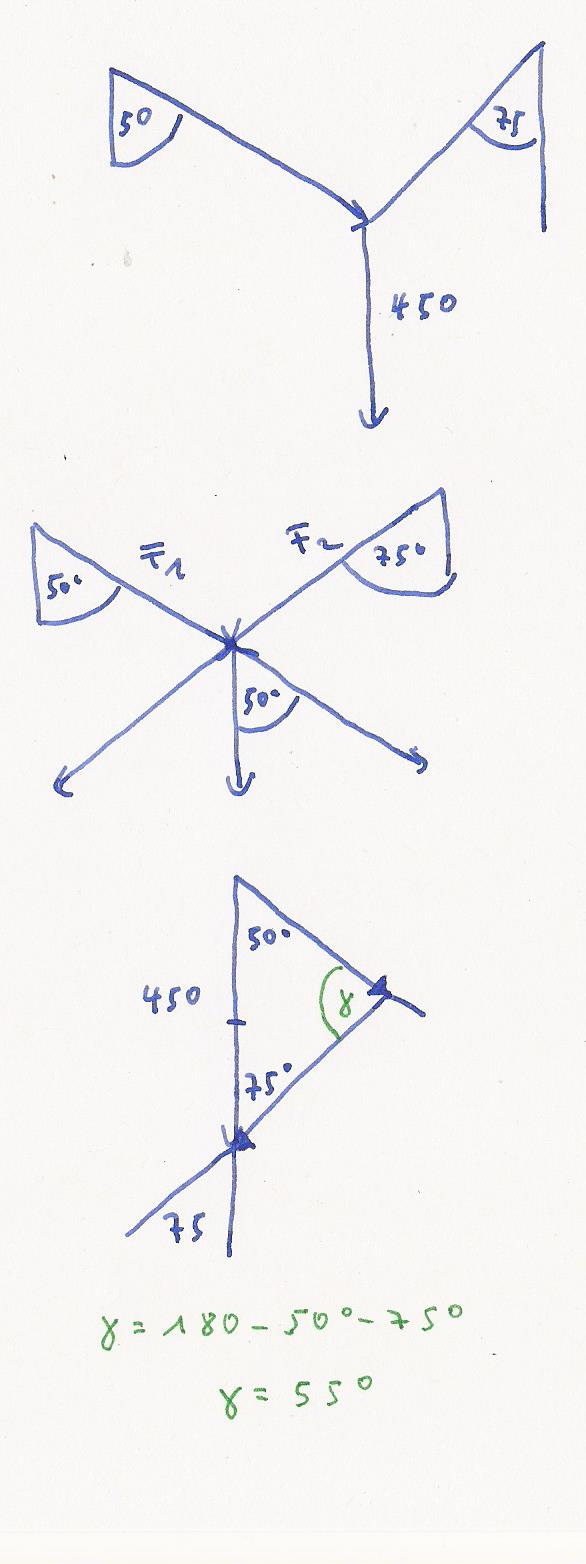
Die erste Skizze zeigt dir den Sachverhalt in real.
m = 45 kg
F = 450 N ( vereinfachend )

Die zweite Skizze zeigt dir die Aufteilung in die
Kräfte F1 und F2.

Die dritte Skizze ein Dreieck. Oben rechts
wäre die Kraft F1; unten rechts die Kraft F2.

Die Winkelsumme im Dreieck ist 180 °.
Gamma = 180 - 50 - 75 = 55 °

Jetzt wird nach dem Sinussatz weitergerechnet.
Zum sinussatz siehe den Link.
https://www.matheretter.de/wiki/sinussatz

sin ( gamma ) / c = sin ( beta ) / b
sin (55) / 450 = sin(75) / F2
F2 = sin (75) * 450 / sin (55)
F2 = 531 N

sin ( gamma ) / c = sin ( alpha ) / a
sin (55) / 450 = sin(50) / F1
F1 = sin (50) * 450 / sin (55)
F2 = 421 N

Das Ganze ist schon etwas schwieriger.

mfg Georg

Answer 2

Ok, dann will ich mal versuchen. Zunächst hilft sicher eine Skizze, darin würde ich Kind, Seile, Mauern und die beteiligten Winkel vorsehen. Weiter würde ich noch die Kraftvektoren hinzunehmen, also die senkrecht nach unten gerichtete Gewichtskraft des Kindes und die entlang der Seile nach oben gerichteten Haltekräfte. Die Summe der Kraftvektoren muss Null sein. Die Kraftvektoren lassen sich durch Parallelverschiebung zu einem Dreieck zusammenschieben, dessen eine Seite durch den Gewichtskraftvektor gebildet wird. Die beiden Innenwinkel an diesem Gewichtskraftvektor sind aus geometrischen Gründen jeweils so groß wie die beiden gegebenen Seil-Mauer-Winkel. Damit kann der WSW-Kongruenzsatz für Dreiecke zur Konstruktion oder zur Berechnung der beiden anderen Seiten herangezogen werden. Wie es weitergeht hängt nun davon ab, wie ihr das machen sollt.