Funktionen und Graphen: Achsschnittpunkte, Steigungsfaktoren und Lösungswerte

Question

habe absolute Probleme mit einer Aufgabe:

Gleichung 1:  4x-2y=0

Gleichung 2:  3x-1,5y=

Aufgabenstellung a)  ermitteln der Achsschnittpunkte

                                 b)  ermitteln der Steigungsfaktoren und Lösungswerte

Habe schon alle 3 Rechenwege ausprobiert komme aber auf kein Ergebnis.

Rechenwege: Additionsverfahren, Einsetzungsverfahren, Gleichsetzungsverfahren.

Es währe schön wenn mir jemand helfen kann.

 

MfG

Comments

Bei Gleichung 2 fehlt noch eine Zahl: 3x-1,5y = ?

Welche ist das?

---

Für beide Gleichungunge erst einmal Äquivalenzumformungen vornehmen ( Annahme 2. Gleichung auch 0).

Dann:

1.      4x-2y=0     ⇒ 4x=2y            ⇒        y=2x      

Schnittpunkt mit den Achsen liegt im Punkt (0/0)

 und die Steigung ist 2

 Wertetabelle anlegen      x      -2    -1    0    1     2

                                         y      -4    -2    0     2    4

2.  3x-1,5y= 0    ⇒  3x=1,5y             ⇒     y=2x

 Erste lieare Gleichung ist ist identisch mit der 2. linearen Gleichung.

Ich Hoffe jetz ist besser erkennbar.

---

Ich habe bei der 2. Gleichung die Zahl 6 als Ergebnis vergessen.

MfG

---

Hallo Akelei !

Danke für die Hilfe, aber leider ist in der 2. Gleichung das Ergebnis 6. Wie kommt man den darauf, und kann man das Minus vor 2y einfach weglassen?

---

Hallo Akelei, vergiss diesen Komentar einfach da habe ich mich ja eben richtig blöd angestellt mit der Frage! Ich danke

nochmals es war sehr hilfreich!

MfG

Answer 1

Gleichung 1:  4x - 2y = 0

Gleichung 2:  3x - 1,5y = 6

 

Umstellen der 1. Gleichung nach y:

4*x - 2*y = 0   | -4*x

-2*y = 0 - 4*x

-2*y = - 4*x   | :(-2)

y = - 4*x :(-2)

y = 2*x

 

Umstellen der 2. Gleichung nach y:

3*x - 1,5*y = 6   | -3*x

-1,5*y = 6 - 3*x

-1,5*y = 6 - 3*x  | :(-1,5)

y = 6:(-1,5) - 3*x:(-1,5)

y = -4 + 2*x

y = 2*x - 4

 

Da beide Funktionsgleichungen die Steigung 2 haben (der Wert vor dem x), sind sie parallel. Siehe Grafik: 

 

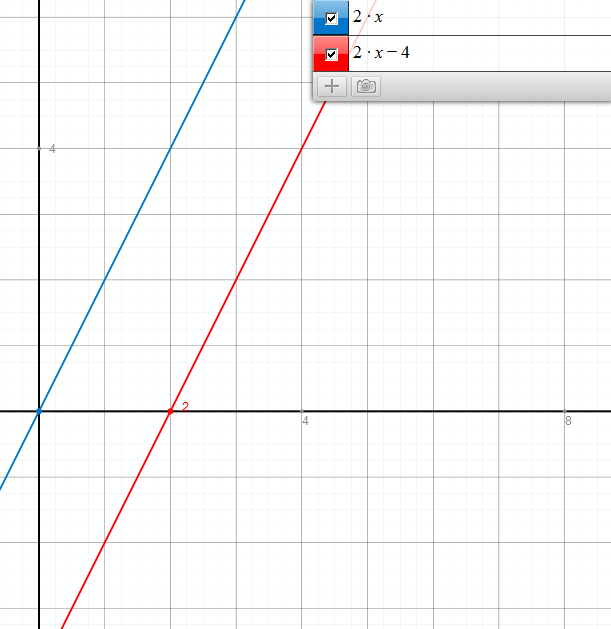
Es gibt also keinen Schnittpunkt, daher findest du auch keine rechnerische Lösung für einen Schnittpunkt.

Schnittpunkte berechnest du, indem du die Funktionsgleichungen gleichsetzt:

f(x) = g(x)

y  = y 

2*x = 2*x - 4    |-2x

0 = 4

→ falsche Aussage → keine Lösung für x

 

Gleiches passiert beim Verfahren Lösen mit dem Linearen Gleichungssystem hier erhältst du ebenfalls kein Ergebnis für x.

 

Einführungs-Video zu den LGS:

 

Comments

Danke, ihr habt echt weitergeholfen meine Gedankengänge waren da wohl komplett falsch.

Also nochmals  

MfG