Ganzrationale Funktion dritten Grades mit Hochpunkt im Ursprung.

Question

Bestimme die Gleichung einer ganzrationalen Funktion dritten Grades, deren Graph im Ursprung einen Hochpunkt besitzt und durch die Punkte A(1/0) und B(2/4) verläuft.

Answer 1

Hallo marinaaa,

ganzrationale Funktion 3. Grades:
f(x) = ax³ + bx² + cx + d
f'(x) = 3ax² + 2bx + c

Im Ursprung einen Hochpunkt, also f(0) = 0 und f'(0) = 0:
I. f(0) = a * 0³ + b * 0² + c * 0 + d = 0 | d = 0
II. f'(0) = 3a * 0² + 2b * 0 + c = 0 | c = 0

Geht durch den Punkt A(1|0), also
III. f(1) = a + b + c + d = 0 | a + b = 0

Geht durch den Punkt B(2|4), also
IV. f(2) = 8a + 4b + 2c + d = 4

Da c und d beide = 0, haben wir noch die beiden vereinfachten Gleichungen III. und IV.:
III. a + b = 0
IV. 8a + 4b = 4

IV. - 4 * III. ergibt
4a = 4 | a = 1
Dies eingesetzt in III.
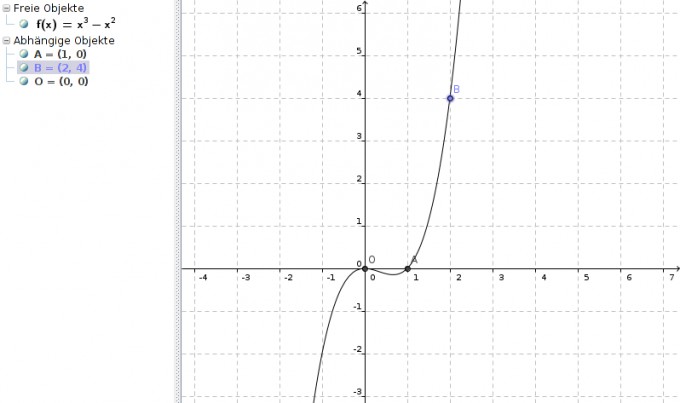
1 + b = 0 | b = -1

Die Funktionsgleichung lautet also
f(x) = x³ - x²


Besten Gruß

Answer 2

y = x³-x²

Comments

Und wie komm ich darauf ?

---

Man kann sich das erarbeiten (s.o.); ich habe es (bei den Zahlen) im Kopf gerechnet.

Answer 3

Hi marinaaa,

Bedingungen auslesen:

f(0)=0

f'(0) = 0

f(1)=0

f(2)=4

Aufstellen auf Grundlage von f(x) = ax^3+bx^2+cx+d

d = 0

c = 0

a + b + c + d = 0

8a + 4b + 2c + d = 4

Es ergibt sich f(x) = x^3 - x^2

Grüße

Comments

Gerne ;)    .

Answer 4

Bestimme die Gleichung einer ganzrationalen Funktion dritten Grades, deren Graph im Ursprung einen Hochpunkt besitzt und durch die Punkte \(A(1|0) \)  und \(B(2|4)\) verläuft.

\(f(x)=a*x^2(x-1)\)

\(B(2|4)\):

\(f(2)=a*4(2-1)=4a=4\)   \(a=1\)

\(f(x)=x^2(x-1)\)