Gib die Gleichung der Tangenten an, die von dem Punkt P(2/-8) an f(x)= x^3-4x gelegt werden

Question

ich weiß leider überhaupt gar nicht wie ich diese Aufgabe rechnen soll.

Es wäre super wenn mir irgendjemand einen Lösungsweg aufzeigen könnte:)

schonmal vielen Dank

Answer 1

f(x) = x^3 - 4·x

(f(x) - (-8)) / (x - 2) = f'(x) Das ist nur der Ansatz. Ausrechnen solltest du es

x = 3 ∨ x = 0 Kontroll-Lösung. wenn du etwas anderes heraus bekommst dann bitte Rücksprache halten.

Tangenten ungeprüft

y = f'(3) * (x - 3) + f(3) = 23·x - 54

y = f'(0) * (x - 0) + f(0) = - 4·x

Comments

Vielen Dank erstmal für die schnelle Antwort!

ich versteh leider deinene Ansatz noch nicht ganz...
nimmst du die erste Ableitung?
das wäre ja dann :
f(x)= x³ -4x
f´(x)=3x² -4

---

Ja genau. Das müsstest du im Ansatz für f(x) und f'(x) einsetzen und das Ganze dann nach x auflösen.

---

ist des falsch wenn ich denke:

ich brauche die steigung an dem punkt P. darum leite ich die Funktion ab und setzte meinen punkt in die ableitung ein und hab dann schon die steigung der tangente ( y=mx+c).
so haben wir bis jetzt immer die aufaben gelöst...

vielen dank für deine hilfe!!

---

Ja das ist verkehrt. Bisher war der Punkt P immer euer Tangentenpunkt auf dem Graphen. Jetzt befindet sich aber P nicht auf dem Graphen sondern daneben.

Daher ist es unnutz die Steugung am Punkt P zu berechnen. Am besten machst du dir mal eine Skizze. Zeichne den Graphen und Punkt P und dann legst du mal mit dem Lineal eine Gerade durch P die eine Tangente an den Graphen ist.

---

aaah okay jetzt hab ichs verstanden !!!

suuper viielen dank fürs erklären!!
und die schnellen antworten!

Liebe Grüße :)

Answer 2

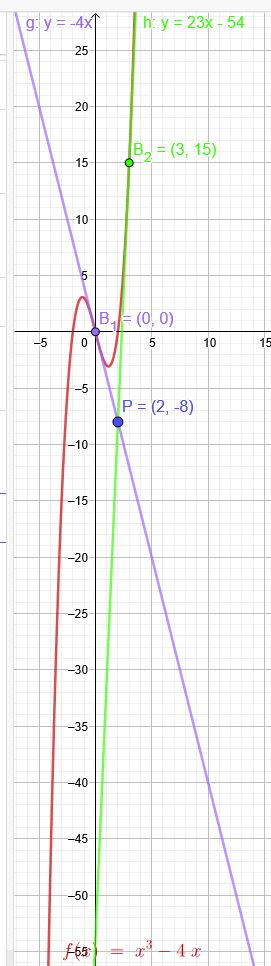
Gib die Gleichungen der Tangenten an, die von dem Punkt \(P(\blue{2}|-\red{8})\)  an \(f(x)= x^3-4x\) gelegt werden.

\(f´(x)= 3x^2-4\)  Berührpunkte sind

\(B(x|x^3-4x)\)

\( \frac{x^3-4x+\red{8}}{x-\blue{2}}=3x^2-4 \)

\( x^3-4x+8=3x^3-6x^2-4x +8\)

\( x^3-3x^2=0 \)

\( x^2\cdot(x-3)=0 \)

1.) \(x=0\)   \(f(0)= 0\)  \(f´(0)=-4\)

2.) \(x=3\)    \(f(3)=27-12=15\)    \(f´(3)= 23\)

Nun die Tangenten bestimmen.